题目内容
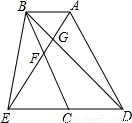
(2001•苏州)如图,已知E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G.(1)求证:△AFB≌△EFC;(2)若BD=12cm,求DG的长.

【答案】分析:(1)根据平行四边形性质推出AB=CD=CE,AB∥CD,推出∠ABF=FCE,∠BAF=∠FEC,根据全等三角形的判定证出即可;
(2)求出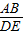 =
= =
= ,把BD的长代入求出即可.
,把BD的长代入求出即可.
解答:(1)证明:在平行四边形ABCD中,
∵AB∥CD,
∴∠BAF=∠CEF,∠ABF=∠ECF,
∵AB=CD,CE=CD,
∴AB=CE,
在△AFB和△EFC中
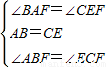 ,
,
∴△AFB≌△EFC.
(2)解:∵ED=2CD=2AB,
∴ ,
,
∵AB∥CD,
∴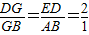 ,
,
又∵BD=12,
∴DG= BD=8cm,
BD=8cm,
答:DG的长是8cm.
点评:本题考查了平行四边形的性质,平行线的性质,全等三角形的判定,平行线分线段成比例定理等知识点,主要考查学生能否根据性质进行推理,题目比较典型,难度也适中.
(2)求出
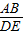 =
= =
= ,把BD的长代入求出即可.
,把BD的长代入求出即可.解答:(1)证明:在平行四边形ABCD中,
∵AB∥CD,
∴∠BAF=∠CEF,∠ABF=∠ECF,
∵AB=CD,CE=CD,
∴AB=CE,
在△AFB和△EFC中
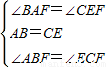 ,
,∴△AFB≌△EFC.
(2)解:∵ED=2CD=2AB,
∴
 ,
,∵AB∥CD,
∴
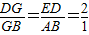 ,
,又∵BD=12,
∴DG=
 BD=8cm,
BD=8cm,答:DG的长是8cm.
点评:本题考查了平行四边形的性质,平行线的性质,全等三角形的判定,平行线分线段成比例定理等知识点,主要考查学生能否根据性质进行推理,题目比较典型,难度也适中.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
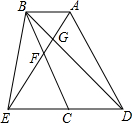 (2001•苏州)如图,已知E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G.
(2001•苏州)如图,已知E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G.