题目内容
AB是⊙O的弦,∠AOB=80°,则弦AB所对的圆周角是( )
| A、40° | B、140°或40° | C、20° | D、20°或160° |
分析:此题要分两种情况:当圆周角的顶点在优弧上时;当圆周角的顶点在劣弧上时;通过分析,从而得到答案.
解答: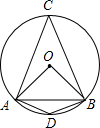 解:当圆周角的顶点在优弧上时,根据圆周角定理,得圆周角:
解:当圆周角的顶点在优弧上时,根据圆周角定理,得圆周角:
∠ACB=
∠AOB=
×80°=40°;
当圆周角的顶点在劣弧上时,根据圆内接四边形的性质,得此圆周角:
∠ADB=180°-∠ACB=180°-40°=140°;
所以弦AB所对的圆周角是40°或140°.
故选B.
 解:当圆周角的顶点在优弧上时,根据圆周角定理,得圆周角:
解:当圆周角的顶点在优弧上时,根据圆周角定理,得圆周角:∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
当圆周角的顶点在劣弧上时,根据圆内接四边形的性质,得此圆周角:
∠ADB=180°-∠ACB=180°-40°=140°;
所以弦AB所对的圆周角是40°或140°.
故选B.
点评:注意:弦所对的圆周角有两种情况,且两种情况的角是互补的关系.

练习册系列答案
相关题目
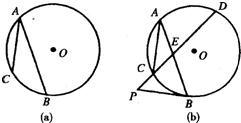 14、如图,已知AC、AB是⊙O的弦,AB>AC.
14、如图,已知AC、AB是⊙O的弦,AB>AC.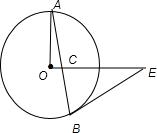
 如图,AB是⊙0的弦,BC与⊙0相切于点B,连接OA、OB.若∠ABC=70°,则∠A等于
如图,AB是⊙0的弦,BC与⊙0相切于点B,连接OA、OB.若∠ABC=70°,则∠A等于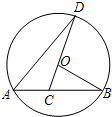 如图,已知AB是⊙O的弦,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长,CO交⊙O于点D,连接AD.若∠B=30°,∠D=20°,则∠BOD的度数为
如图,已知AB是⊙O的弦,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长,CO交⊙O于点D,连接AD.若∠B=30°,∠D=20°,则∠BOD的度数为