题目内容
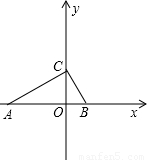
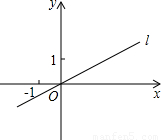
(2004•黑龙江)如图,在平面直角坐标系中,直线l的解析式为y=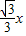 ,关于x的一元二次方程2x2-2(m+2)x+(2m+5)=0(m>0)有两个相等的实数根.
,关于x的一元二次方程2x2-2(m+2)x+(2m+5)=0(m>0)有两个相等的实数根.(1)试求出m的值,并求出经过点A(0,-m)和D(m,0)的直线解析式;
(2)在线段AD上顺次取两点B、C,使AB=CD=
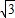 -1,试判断△OBC的形状;
-1,试判断△OBC的形状;(3)设直线l与直线AD交于点P,图中是否存在与△OAB相似的三角形?如果存在,请直接写出;如果不存在,请说明理由.
【答案】分析:(1)依题意得△=0得出m值,然后可求出点A,D的坐标,设直线AD的解析式为y=kx+b,把已知坐标代入可求得解析式;
(2)作OE⊥AD于E,利用勾股定理求出AD,继而求出OE的长.然后根据三角函数证明△OBC为等边三角形;
(3)利用相似三角形的判定可知道存在与△OAB相似的三角形.
解答:解:(1)由题意得△=[-2(m+2)]2-4×2×(2m+5)=0,
∴m=±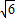 ,
,
∵m>0,
∴m=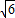 ,
,
∴点A(0,-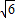 )、D(
)、D(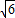 ,0),
,0),
设经过A、D两点的直线解析式为y=kx+b,
则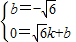 ,
,
解得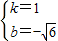 ,
,
∴y=x-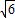 ;
;
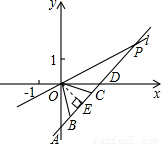
(2)作OE⊥AD于E,
由(1)得OA=OD=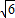 ,
,
∴AD=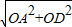 =2
=2 ,
,
∴OE=AE=ED= AD=
AD=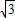 ,
,
∵AB=CD=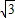 -1,
-1,
∴BE=EC=1,
∴OB=OC,
在Rt△OBE中,tan∠OBE=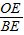 =
= ,
,
∴∠OBC=60°,
∴△OBC为等边三角形;
(3)存在,△ODC、△OPC、△PAO.
点评:本题考查的是相似三角形的判定定理,一次函数的综合运用,等边三角形的性质以及三角函数的有关知识.
(2)作OE⊥AD于E,利用勾股定理求出AD,继而求出OE的长.然后根据三角函数证明△OBC为等边三角形;
(3)利用相似三角形的判定可知道存在与△OAB相似的三角形.
解答:解:(1)由题意得△=[-2(m+2)]2-4×2×(2m+5)=0,
∴m=±
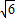 ,
,∵m>0,
∴m=
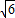 ,
,∴点A(0,-
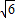 )、D(
)、D(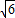 ,0),
,0),设经过A、D两点的直线解析式为y=kx+b,
则
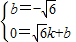 ,
,解得
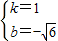 ,
,∴y=x-
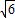 ;
;
(2)作OE⊥AD于E,
由(1)得OA=OD=
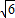 ,
,∴AD=
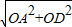 =2
=2 ,
,∴OE=AE=ED=
 AD=
AD=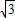 ,
,∵AB=CD=
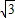 -1,
-1,∴BE=EC=1,
∴OB=OC,
在Rt△OBE中,tan∠OBE=
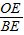 =
= ,
,∴∠OBC=60°,
∴△OBC为等边三角形;
(3)存在,△ODC、△OPC、△PAO.
点评:本题考查的是相似三角形的判定定理,一次函数的综合运用,等边三角形的性质以及三角函数的有关知识.

练习册系列答案
相关题目