题目内容
在9×9的方格表中,共有81个小方格.在每一个小方格中,写上一个数,如果只要每行、每列至多有三个不同的数,就能保证在方格表中存在一个数,这个数在其某一行中至少出现n次,在某一列中也至少出现n次,那么,n的最大值是多少?并证明你的结论.
解:1 2 3
4 5 6
7 8 9
每一格表示3×3的方格,如图的特例中的数字,得到n≤3,猜想:n的最大值为3.
只需要证按条件填好的81个数后一定存在一个数,这个数在某一行至少出现3次,在某一列也至少出现3次.
若某数在某行至少出现3次,就在该数上打“√”作上记号,则每行至少有5个“√”(不打“√”号的最多有4个),因此表格中至少有45个,
同理,若某数在某列至少出现3次,就在该数上打“0”作上记号,则表格中至少有45个“0”.
由于45+45=90,所以至少有一格既打“√”,又打“0”,即这个数在某一行至少出现3次,在某一列至少出现3次.
分析:通过举例首先猜想n的最大值是3,然后通过做标记实验的方法得当某数在某一行至少出现3次,在某一列至少出现3次.
点评:本题考查了规律探究题,解决此类问题的关键是仔细的观察数据之间的关系并发现其中的规律,从而解决问题.
4 5 6
7 8 9
每一格表示3×3的方格,如图的特例中的数字,得到n≤3,猜想:n的最大值为3.
只需要证按条件填好的81个数后一定存在一个数,这个数在某一行至少出现3次,在某一列也至少出现3次.
若某数在某行至少出现3次,就在该数上打“√”作上记号,则每行至少有5个“√”(不打“√”号的最多有4个),因此表格中至少有45个,
同理,若某数在某列至少出现3次,就在该数上打“0”作上记号,则表格中至少有45个“0”.
由于45+45=90,所以至少有一格既打“√”,又打“0”,即这个数在某一行至少出现3次,在某一列至少出现3次.
分析:通过举例首先猜想n的最大值是3,然后通过做标记实验的方法得当某数在某一行至少出现3次,在某一列至少出现3次.
点评:本题考查了规律探究题,解决此类问题的关键是仔细的观察数据之间的关系并发现其中的规律,从而解决问题.

练习册系列答案
相关题目
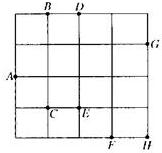 6、在4×4的方格表中给出如图所示的8个点,任选三个作为三角形的顶点,共可构成( )个等腰三角形.
6、在4×4的方格表中给出如图所示的8个点,任选三个作为三角形的顶点,共可构成( )个等腰三角形. 在右图的方格表中填入字母,使得每行、每列及对角线上的四个字母均含有a、b、c、d,则“?”处应填的字母为( )
在右图的方格表中填入字母,使得每行、每列及对角线上的四个字母均含有a、b、c、d,则“?”处应填的字母为( )