题目内容
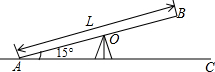（2010•来宾）儿童活动乐园中的跷跷板AB的支撑架位于板的中点O处（如图），一端压下与地面接触于点A，翘起的板与地面AC所成的最大角度为15°，为了安全，要求此时翘起一端的端点B离地面的最大高度是0.8米，最小高度是0.6米，试求出跷跷板的长度L的取值范围（要求列不等式（组）求解，精确到0.01米）．（参考数据：sin15°≈0.259，cos15°≈0.966，tan15°≈0.268）分析：设跷跷板长x米，过点B作BD⊥AC于点D，在直角△ABD中运用三角函数用含x的代数式表示BD，再根据0.6≤BD≤0.8，列出不等式组，解不等式组即可．
解答：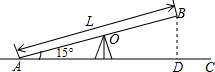
解：设跷跷板长x米，过点B作BD⊥AC于点D．
在直角△ABD中，∵∠ADB=90°，∠BAD=15°，
∴BD=AB•sin∠BAD≈0.259x．
∵0.6≤BD≤0.8，
∴0.6≤0.259x≤0.8，
解得2.32≤x≤3.09．
故跷跷板的长度L的取值范围约是2.32米～3.09米．
解：设跷跷板长x米，过点B作BD⊥AC于点D．在直角△ABD中，∵∠ADB=90°，∠BAD=15°，
∴BD=AB•sin∠BAD≈0.259x．
∵0.6≤BD≤0.8，
∴0.6≤0.259x≤0.8，
解得2.32≤x≤3.09．
故跷跷板的长度L的取值范围约是2.32米～3.09米．
点评：本题考查的是解直角三角形的应用及一元一次不等式组的应用，根据题意作出辅助线，利用锐角三角函数的定义表示出BD的长度是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
（2010•来宾）如图是由若干个相同的小正方体组合而成的几何体，则这个几何体的俯视图是（ ）
（2010•来宾）已知矩形OABC的顶点O在平面直角坐标系的原点，边OA、OC分别在x、y轴的正半轴上，且OA=3cm，OC=4cm，点M从点A出发沿AB向终点B运动，点N从点C出发沿CA向终点A运动，点M、N同时出发，且运动的速度均为1cm/秒，当其中一个点到达终点时，另一点即停止运动．设运动的时间为t秒．