题目内容
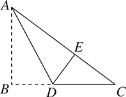
【题目】如图,在平面直角坐标中,抛物线y=ax2-2ax-3a(a≠0)与x轴交于A、B(A在B的左侧),与y轴交于点C,且OC=3OA.
(1)如图(1)求抛物线的解析式;
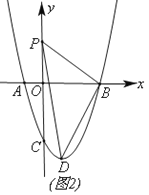
(2)如图(2)动点P从点O出发,沿y轴正方向以每秒1个单位的速度移动,点D是抛物线顶点,连接PB、PD、BD,设点P运动时间为t(单位:秒),△PBD的面积为S,求S与t的函数关系式;
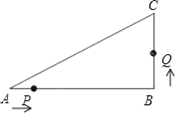
(3)如图(3)在(2)的条件下,延长BP交抛物线于点Q,过点O作OE⊥BQ,垂足为E,连接CE、CB,若CE=CB,求t值,并求出此时的Q点坐标.


【答案】(1)y=x2-2x-3;(2)S=t+6;(3)t=![]() ;Q (
;Q (![]() ,
, ![]() ).
).
【解析】试题分析:(1)令y=0,求出A、B的坐标,再由OC=3OA,得到a的值,即可得到结论;
(2)过B点作QR∥y轴,作PQ⊥DR,垂足为Q,过D点作DH∥x轴,交y轴于点H,交BR于点R.S△PDB=S矩形PQRH-(S△PQB+S△PDH+S△DBR),代入相关数据即可得到结论;
(3)延长EO、BC相交于点F,过F作作FG⊥y轴,垂足为G,ON⊥AD,过Q作QH⊥x轴,垂足为H.可证明△FCG≌△BCO,得到CG=CO=3,FG=BO=3.在△GOF中,可得到tan∠FOG=![]() .由∠OBE=∠FOG,得到tan∠OBE=
.由∠OBE=∠FOG,得到tan∠OBE=![]() ,从而可求的t的值.
,从而可求的t的值.
设点Q(m.m2-2m-3),则QH=m2-2m-3,BH=3-m,得到tan∠OBE=![]() ,BH=2QH,3-m=2(m2-2m-3),即可得到m的值,进而得到Q 的坐标.
,BH=2QH,3-m=2(m2-2m-3),即可得到m的值,进而得到Q 的坐标.
试题解析:解:(1)令y=0,ax2-2ax-3a=0,a(x-3)(x+1)=0.∵a≠0,∴ ![]() ,
, ![]() .∵A在B的左侧,∴A(-1,0),B(3,0).∵OC=3OA=3,∴C(0,-3),∴-3a=-3,∴a=1,
.∵A在B的左侧,∴A(-1,0),B(3,0).∵OC=3OA=3,∴C(0,-3),∴-3a=-3,∴a=1,
∴抛物线为:y=x2-2x-3.
(2)如图(2)过B点作QR∥y轴,作PQ⊥DR,垂足为Q,过D点作DH∥x轴,交y轴于点H,交BR于点R.
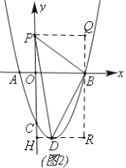
∵D是抛物线定点,∴D(1,-4).∵P(0,
∴PQ=3,BQ=t,BR=4,DR=2,DH=1,PH=t+4,∴S△PDB=S矩形PQRH-(S△PQB+S△PDH+S△DBR)
∴S=PH×PQ-![]() (PQ×BQ+PH×DH+DR ×BR) =(t+4)×3-
(PQ×BQ+PH×DH+DR ×BR) =(t+4)×3-![]() ([3×t+(t+4)×1+2×4]
([3×t+(t+4)×1+2×4]
∴ S=t+6.
(3)如图(3),延长EO、BC相交于点F,过F作作FG⊥y轴,垂足为G,ON⊥AD,
过Q作QH⊥x轴,垂足为H.
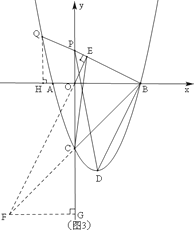
∵OE⊥BQ,∴∠BEF=900.∵CE=CB,∴∠BEC=∠EBC.
∵∠BEC+∠CEF=900,∠EBC+∠BFE=900,∴∠CEF=∠BFE,∴CF=CE=CB.∵FG⊥y轴,∠FGC=∠BOC=900,∠FCG=∠BCO,∴△FCG≌△BCO,∴CG=CO=3,FG=BO=3.
在△GOF中,∠FGC=900,FG=3,OG=6,∴tan∠FOG=![]() .
.
∵∠BOE+∠OBE=900.,∠BOEC+∠POE=900,∴∠OBE=∠POE,∠POE=∠FOG,∴∠OBE=∠FOG,∴tan∠OBE=![]() ,∴OP=
,∴OP= ![]() =
=![]() ,∴t=
,∴t=![]() .
.
设点Q(m.m2-2m-3),则QH=m2-2m-3,BH=3-m,∴tan∠OBE=![]() ,BH=2QH,3-m=2(m2-2m-3),∴m1=
,BH=2QH,3-m=2(m2-2m-3),∴m1=![]() ,m2=3(舍去),∴m=
,m2=3(舍去),∴m=![]() ,∴Q (
,∴Q (![]() ).
).