题目内容
在⊙O中，若
=2
，则弦AB和CD的关系是（ ）
 |
| AB |
|
| CD |
分析：先根据题意画出图形，取
的中点E，连接AE、BE，则
=
=
，故可得出AE=BE=CD，在△ABE中由三角形的三边关系即可得出结论．
|
| AB |
|
| AE |
|
| BE |
|
| CD |
解答：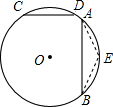
解：如图所示：取
的中点E，连接AE、BE，则
=
=
，
∵
=2
，
∴
=
=
，
∴AE=BE=CD，
在△ABE中由三角形的三边关系可知，AE+BE＞AB，即2CD＞AB．
故选B．
解：如图所示：取 |
| AB |
|
| AE |
|
| BE |
| 1 |
| 2 |
|
| AB |
∵
|
| AB |
|
| CD |
∴
|
| AE |
|
| BE |
|
| CD |
∴AE=BE=CD，
在△ABE中由三角形的三边关系可知，AE+BE＞AB，即2CD＞AB．
故选B．
点评：本题考查的是圆心角、弧、弦的关系及三角形的三边关系，即在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．
练习册系列答案
习题精选系列答案
相关题目
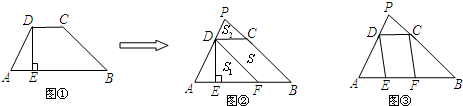
如图，△ABC中，点D是BC中点，连接AD并延长到点E，连接BE．