题目内容
【题目】如图:已知AB∥CD,EF⊥AB于点O,∠FGC=125°,求∠EFG的度数.

下面提供三种思路:
(1)过点F作FH∥AB;
(2)延长EF交CD于M;
(3)延长GF交AB于K.
请你利用三个思路中的两个思路,
将图形补充完整,求∠EFG的度数.
解(一):
解(二):
【答案】见解析
【解析】
试题分析:(一)过点F作FH∥AB,求出∠EFH,求出∠GFH,相加即可;
(二)延长EF交CD于M,求出∠GMF、根据三角形外角性质求出∠GFM,即可求出答案.
解:(一)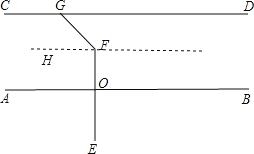
利用思路(1)过点F 作FH∥AB,
∵EF⊥AB,
∴∠BOF=90°,
∵FH∥AB,
∴∠HFO=∠BOF=90°,
∵AB∥CD,
∴FH∥CD,
∴∠FGC+∠GFH=180°,
∵∠FGC=125°,
∴∠GFH=55°,
∴∠EFG=∠GFH+∠HFO=55°+90°=145°;
解:(二)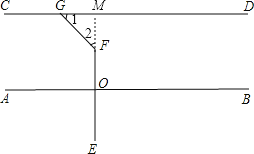
利用思路(2)延长EF交CD于M,
∵EF⊥AB,
∴∠BOF=90°,
∵CD∥AB,
∴∠CMF=∠BOF=90°,
∵∠FGC=125°,
∴∠1=55°,
∵∠1+∠2+∠GMF=180°,
∴∠2=35°,
∵∠GFO+∠2=180°,
∴∠GFO=145°.

练习册系列答案
相关题目
