题目内容
如图，直线AB切⊙O于点C，∠OAC=∠OBC，则下列结论错误的是（ ）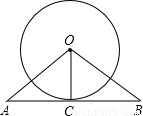
A．OC是△ABO中AB边上的高
B．OC所在直线是△ABO的对称轴
C．OC是∠AOB平分线
D．AC＞BC
【答案】分析：利用切线性质得OC⊥AB，再利用等腰三角形的性质分析，即可求解．
解答：解：∵∠OAC=∠OBC，
∴由等角对等边得OA=OB，
∵直线AB切⊙O于点C，
∴OC⊥AB，
由等腰三角形的底边上的高与底边上的中线，顶角的平分线重合知．
A、B、C均正确，
D错误，应为AC=BC．
故选D．
点评：本题利用了切线的性质，等腰三角形的性质求解．
解答：解：∵∠OAC=∠OBC，
∴由等角对等边得OA=OB，
∵直线AB切⊙O于点C，
∴OC⊥AB，
由等腰三角形的底边上的高与底边上的中线，顶角的平分线重合知．
A、B、C均正确，
D错误，应为AC=BC．
故选D．
点评：本题利用了切线的性质，等腰三角形的性质求解．
练习册系列答案
相关题目
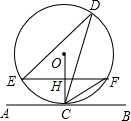如图，直线AB切⊙O于C点，D是⊙O上一点，∠EDC=30°，弦EF∥AB，连接OC交EF于H点，连接CF，且CF=2，则HE的长为
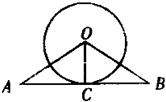10、如图，直线AB切⊙O于点C，∠OAC=∠OBC，则下列结论错误的是（ ）
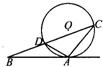1、如图，直线AB切⊙O于点A，割线BDC交⊙O于点D、C．若∠C=30°，∠B=20°，则∠ADC=（ ）