题目内容
.(10分)如图9,正方形ABCD边长为10cm,P、Q分别是BC、CD上的两个动点,当P 点在BC上运动时,且A P⊥PQ.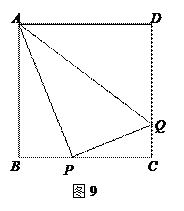
(1)求证:△ABP∽△PCQ;
(2)当BP等于多少时,四边形ABCQ的面积为62cm2.
(1)△ABP∽△PCQ,证明略。
(2)当BP等于4cm或6cm时,四边形ABCQ的面积为62cm2解析:
(1)在正方形ABCD中,AB=BC=CD=AD=10,∠B=∠C=90°,
∵ AP⊥PQ,∴∠APQ=90°,∴ ∠APB+∠CPQ=90°.
在Rt△ABP中,∠APB+∠BAP=90°,∴∠BAP=∠CPQ . ∴ △ABP∽△PCQ .
(2)解法1:设BP=x. ∵ △ABP∽△PCQ,∴
 ,
,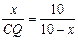 ,
,∴
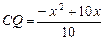 , ∴
, ∴ 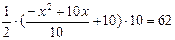 .
.整理,得x2-10x+24=0. 解得x1=4,x2=6.
∴ 当BP等于4cm或6cm时,四边形ABCQ的面积为62cm2.
解法2:设BP=x. ∵ SRt△ADQ=S正方形ABCD-S四边形ABCQ=100-62=38.
∴
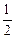 AD·DQ=38,∴ DQ=
AD·DQ=38,∴ DQ=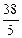 ,∴ QC=CD-DQ=10-
,∴ QC=CD-DQ=10-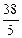 =
=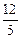
∵ △ABP∽△PCQ,∴
 ,
,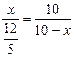 ,
,整理,得x2-10x+24=0. 解得x1=4,x2=6.
∴ 当BP等于4cm或6cm时,四边形ABCQ的面积为62cm2.

练习册系列答案
相关题目
 3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.

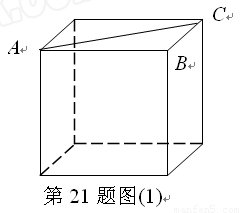

 与平面展开图中
与平面展开图中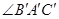 的大小关系?
的大小关系?