题目内容
【题目】如图,△ABC中,DE∥AB,EF∥AB,∠BED=∠CEF,
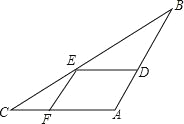
(1)试说明△ABC是等腰三角形,
(2)探索AB+AC与四边形ADEF的周长关系.
【答案】(1)说明见解析;(2)AC+AB=四边形EFAD的周长.
【解析】
试题分析:(1)由平行线的性质可得∠EAD=∠F,∠BAF=∠E,进而再通过角之间的转化得出结论;
(2)由平行线的性质可得∠EAD=∠F,∠BAF=∠E,由于∠BED=∠CEF,得到∠C=∠CEF=∠BED=∠B,于是得到EF=CF,DE=DB,即可得到结论.
试题解析:(1)∵DE∥AC
∴∠BED=∠C,
∵EF∥AB,
∴∠CEF=∠B,
∵∠BED=∠CEF,
∴∠B=∠C,
∴△ABC是等腰三角形;
(2)AB+AC=四边形ADEF的周长,
理由:∵DE∥AC,
∴∠BED=∠C,
∵EF∥AB,
∴∠CEF=∠B,
∵∠BED=∠CEF,
∴∠C=∠CEF=∠BED=∠B,
∴EF=CF,DE=DB,
∴AC+AB=CF+AF+AD+BD=EF+AF+AD+DE=四边形EFAD的周长.

练习册系列答案
相关题目