题目内容
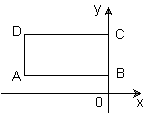
如图,矩形AOCD中,D点的坐标为( ,3),OC边在x轴上,点F是OC边上的动点,并且∠AFE=90°,点
,3),OC边在x轴上,点F是OC边上的动点,并且∠AFE=90°,点 E在CD边上,设OF=x,CE=y.
E在CD边上,设OF=x,CE=y.(1)求y与x的函数关系式;
(2)当CE的值最大时求点F的坐标;
(3)在(2)的条件下,判定以AE为直径的圆与OC边的位置关系.
【答案】分析:(1)根据点D的坐标求出OA、OC的长,再根据同角的余角相等求出∠OAF=∠EFC,然后利用两角对应相等,两三角形相似求出△AOF和△FCE相似,再根据相似三角形对应边成比例列式整理即可得解;
(2)根据二次函数的最值问题求出CE最大时的x的值,从而得到点F的坐标;
(3)取AE的中点P,然后判定PE为梯形AOCE的中位线,根据梯形的中位线平行于底边可得PE⊥OC,再根据直角三角形斜边上的中线等于斜边的一半可得PF= AE,然后根据直线与圆的位置关系解答.
AE,然后根据直线与圆的位置关系解答.
解答:解:(1)∵D点的坐标为(2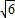 ,3),
,3),
∴OA=3,OC=2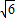 ,
,
∵∠AFE=90°,
∴∠AFO+∠EFC=90°,
又∵∠AFO+∠OAF=90°,
∴∠OAF=∠EFC,
又∵∠AOF=∠FCE=90°,
∴△AOF∽△FCE,
∴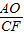 =
=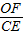 ,
,
即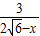 =
=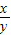 ,
,
整理得,y=- x2+
x2+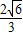 x;
x;
(2)∵y=- x2+
x2+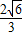 x,
x,
=- (x2-2
(x2-2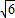 x+6)+2,
x+6)+2,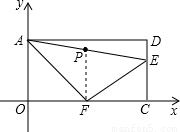
=- (x-
(x-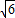 )2+2,
)2+2,
∴当x=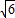 ,即OF=
,即OF=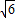 时,CE有最大值,为2,
时,CE有最大值,为2,
此时点F的坐标为(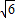 ,0);
,0);
(3)取AE的中点P,
∵点F的坐标为(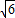 ,0),
,0),
∴OF=CF= OC=
OC=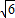 ,
,
∴PF为梯形AOCE的中位线,
∴PF⊥OC,
又∵∠AFE=90°,
∴PF= AE,
AE,
∴以AE为直径的圆与OC边相切.
点评:本题考查了圆的综合题型,主要利用了相似三角形的判定与性质,二次函数的最值问题,直角三角形斜边上的中线等于斜边的一半的性质,直线与圆的位置关系,梯形的中位线定理,综合性较强,但难度不大,(3)作辅助线是解题的关键.
(2)根据二次函数的最值问题求出CE最大时的x的值,从而得到点F的坐标;
(3)取AE的中点P,然后判定PE为梯形AOCE的中位线,根据梯形的中位线平行于底边可得PE⊥OC,再根据直角三角形斜边上的中线等于斜边的一半可得PF=
 AE,然后根据直线与圆的位置关系解答.
AE,然后根据直线与圆的位置关系解答.解答:解:(1)∵D点的坐标为(2
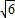 ,3),
,3),∴OA=3,OC=2
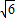 ,
,∵∠AFE=90°,
∴∠AFO+∠EFC=90°,
又∵∠AFO+∠OAF=90°,
∴∠OAF=∠EFC,
又∵∠AOF=∠FCE=90°,
∴△AOF∽△FCE,
∴
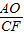 =
=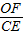 ,
,即
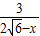 =
=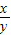 ,
,整理得,y=-
 x2+
x2+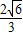 x;
x;(2)∵y=-
 x2+
x2+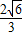 x,
x,=-
 (x2-2
(x2-2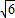 x+6)+2,
x+6)+2,
=-
 (x-
(x-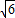 )2+2,
)2+2,∴当x=
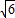 ,即OF=
,即OF=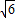 时,CE有最大值,为2,
时,CE有最大值,为2,此时点F的坐标为(
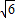 ,0);
,0);(3)取AE的中点P,
∵点F的坐标为(
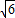 ,0),
,0),∴OF=CF=
 OC=
OC=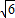 ,
,∴PF为梯形AOCE的中位线,
∴PF⊥OC,
又∵∠AFE=90°,
∴PF=
 AE,
AE,∴以AE为直径的圆与OC边相切.
点评:本题考查了圆的综合题型,主要利用了相似三角形的判定与性质,二次函数的最值问题,直角三角形斜边上的中线等于斜边的一半的性质,直线与圆的位置关系,梯形的中位线定理,综合性较强,但难度不大,(3)作辅助线是解题的关键.

练习册系列答案
相关题目
 13、如图,矩形AOCD中,A、C坐标分别为(-4,0)、(0,2),则D点坐标是
13、如图,矩形AOCD中,A、C坐标分别为(-4,0)、(0,2),则D点坐标是 E在CD边上,设OF=x,CE=y.
E在CD边上,设OF=x,CE=y.