题目内容
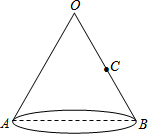 如图,一圆锥的轴截面是边长为6的等边三角形OAB,现有一小虫从点A 爬到OB的中点C处,那么小虫所走的最短路线是多少?
如图,一圆锥的轴截面是边长为6的等边三角形OAB,现有一小虫从点A 爬到OB的中点C处,那么小虫所走的最短路线是多少?
解:圆锥底面是以AB为直径的圆,圆的周长是ABπ=6π,
以OA为一边,将圆锥展开,就得到一个以O为圆心,以OA为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则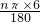 =6π,
=6π,
解得:n=180,
即展开后∠BOA= ×180°=90°,
×180°=90°,
OC= OB=3,OA=6,
OB=3,OA=6,
则在圆锥的侧面上从A点到C点的最短路线的长就是展开后线段AC的长,
由勾股定理得:AC= =
=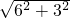 =3
=3 .
.
答:小虫所走的最短路线是3 .
.
分析:求出圆锥底面圆的周长,则以OA为一边,将圆锥展开,就得到一个以O为圆心,以OA为半径的扇形,根据弧长公式求出展开后扇形的圆心角,求出展开后∠BOA=90°,连接AC,根据勾股定理求出AC即可.
点评:本题考查了圆锥的计算,平面展开-最短路线问题,勾股定理,弧长公式等知识点的应用,主要考查学生的理解能力和空间想象能力,题目是一道具有代表性的题目,有一定的难度.
以OA为一边,将圆锥展开,就得到一个以O为圆心,以OA为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则
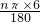 =6π,
=6π,解得:n=180,
即展开后∠BOA=
 ×180°=90°,
×180°=90°,OC=
 OB=3,OA=6,
OB=3,OA=6,则在圆锥的侧面上从A点到C点的最短路线的长就是展开后线段AC的长,
由勾股定理得:AC=
 =
=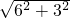 =3
=3 .
.答:小虫所走的最短路线是3
 .
.分析:求出圆锥底面圆的周长,则以OA为一边,将圆锥展开,就得到一个以O为圆心,以OA为半径的扇形,根据弧长公式求出展开后扇形的圆心角,求出展开后∠BOA=90°,连接AC,根据勾股定理求出AC即可.
点评:本题考查了圆锥的计算,平面展开-最短路线问题,勾股定理,弧长公式等知识点的应用,主要考查学生的理解能力和空间想象能力,题目是一道具有代表性的题目,有一定的难度.

练习册系列答案
相关题目
下列结论不正确的是( )
A、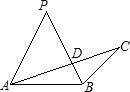 如图,若PA=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=4,PD=3,则AD•DC等于6 | B、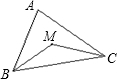 M是△ABC的内心,∠BMC=130°,则∠A的度数为50° | C、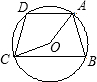 如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于80° | D、若一圆锥的轴截面是等边三角形,则其侧面展开图的圆心角是120° |
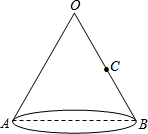 如图,一圆锥的轴截面是边长为6的等边三角形OAB,现有一小虫从点A 爬到OB的中点C处,那么小虫所走的最短路线是多少?
如图,一圆锥的轴截面是边长为6的等边三角形OAB,现有一小虫从点A 爬到OB的中点C处,那么小虫所走的最短路线是多少?