题目内容
如图，等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过⊙O2的圆心O2，连接AO1并延长交⊙O1于点C，则∠ACO2的度数为（ ）| A、60° | B、45° | C、30° | D、20° |
练习册系列答案
相关题目
如图，AB是⊙O的直径，PA切⊙O于点A，PO交⊙O于点C，连结BC．若∠P=36°，则∠B等于（ ）| A、27° | B、30° | C、36° | D、54° |
半径分别为5cm和8cm的两圆相交，则它们的圆心距可能是（ ）
| A、1cm | B、3cm | C、8cm | D、13cm |
如图，⊙A、⊙B的圆心在直线l上，两圆半径都为1cm，圆心距AB=6cm，现⊙A、⊙B同时沿直线l以每秒2cm的速度相向移动，则当两圆第一次相切时，⊙A运动的时间为（ ）| A、1秒 | B、2秒 | C、3秒 | D、1秒或3秒 |
已知⊙O1和⊙O2相切，两圆的圆心距为9cm，⊙O1的半径为4cm，则⊙O2的半径为（ ）
| A、5cm | B、13cm | C、9 cm 或13cm | D、5cm 或13cm |
正六边形的边心距为
，则该正六边形的边长是（ ）
| 3 |
A、
| ||
| B、2 | ||
| C、3 | ||
D、2
|
⊙O的半径等于3，则⊙O的内接正方形的边长等于（ ）
| A、3 | ||
B、2
| ||
C、3
| ||
| D、6 |
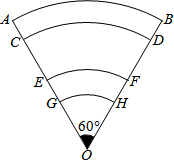如图， |
| AB |
|
| CD |
|
| EF |
|
| GH |
|
| CD |
|
| EF |
| A、π | ||
B、
| ||
C、
| ||
D、
|
圆锥体的底面半径为2，侧面积为8π，则其侧面展开图的圆心角为（ ）
| A、90° | B、120° | C、150° | D、180° |