Question

已知：射线OF交⊙O于点B，半径OA⊥OB，P是射线OF上的一个动点（不与O、B重合），直线AP交⊙O于D，过D作⊙O的切线交射线OF于E．
（1）图a是点P在圆内移动时符合已知条件的图形，在点P移动的过程中，请你通过观察、测量、比较，写出一条与△DPE的边、角或形状有关的规律，并说明理由；
（2）请你在图b中画出点P在圆外移动时符合已知条件的图形，第（1）题中发现的规律是否仍然存在？说明理由．

Answer 1

【答案】分析：（1）可运用DE时圆O的切线来求解．连接OD，那么OD⊥DE，∠ODA+∠PDE=90°，因为OA=OD，那么∠OAD=∠ODA．在直角三角形OAP中，∠OAP+∠OPA=90°，那么∠EDP=∠APO，由于∠EPD和∠APO是对顶角，因此∠EDP=∠EPD，即三角形PED是等腰三角形；
（2）应该符合，和（1）的证法完全一样，也是通过将相等角进行转换，然后根据等角的余角相等来得出∠EDP=∠EPD．
解答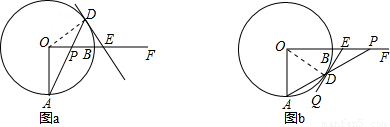：解：（1）△DPE是等腰三角形
证明：连接OD，
∴OD⊥DE，OA=OD，
∴∠ODA+∠PDE=90°，∠A=∠ODA，
∴∠PDE+∠A=90°；
∵∠A+∠OPA=90°，
而∠OPA=∠DPE，
∴∠A+∠DPE=90°，
∴∠EDP=∠EPD，
即三角形DEP是等腰三角形；

（2）符合．
证明：连接OD，
∴OD⊥DE，OA=OD，
∴∠ODA+∠QDA=90°，∠A=∠ODA，
∴∠QDA+∠A=90°；
∵∠QDA=∠EDP，
∴∠A+∠EDP=90°，
∵∠A+∠OPA=90°，
∴∠EDP=∠OPA．
即三角形DEP是等腰三角形．
点评：本题主要是考查了切线的应用，将相等的角进行转换然后根据等角的余角相等得出结论是本题求解的基本思想．