题目内容
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.

(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
【答案】y=﹣![]() (x﹣6)2+2.6,h≥
(x﹣6)2+2.6,h≥![]()
【解析】
试题分析:(1)利用h=2.6将点(0,2),代入解析式求出即可;
(2)利用当x=9时,y=﹣![]() (x﹣6)2+2.6=2.45,当y=0时,
(x﹣6)2+2.6=2.45,当y=0时,![]() ,分别得出即可;
,分别得出即可;
(3)根据当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),以及当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2)时分别得出h的取值范围,即可得出答案.
试题解析:解:(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x﹣6)2+h过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a=﹣![]() ,
,
故y与x的关系式为:y=﹣![]() (x﹣6)2+2.6,
(x﹣6)2+2.6,
(2)当x=9时,y=﹣![]() (x﹣6)2+2.6=2.45>2.43,
(x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,![]() ,
,
解得:x1=6+2![]() >18,x2=6﹣2
>18,x2=6﹣2![]() (舍去)
(舍去)
故会出界;
(3)当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
![]() ,
,
解得: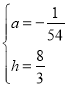 ,
,
此时二次函数解析式为:y=﹣![]() (x﹣6)2+
(x﹣6)2+![]() ,
,
此时球若不出边界h≥![]() ,
,
当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
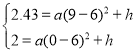 ,
,
解得: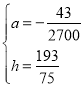 ,
,
此时球要过网h≥![]() ,
,
故若球一定能越过球网,又不出边界,h的取值范围是:h≥![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
