题目内容
中踏销售某种商品,每件进价为10元,在销售过程中发现,平均每天的销售量y(件)与销售价x(元/件)之间的关系可近似的看做一次函数:y=-2x+60;
(1)求中踏平均每天销售这种商品的利润w(元)与销售价x之间的函数关系式;
(2)当这种商品的销售价为多少元时,可以获得最大利润?最大利润是多少?
(1)求中踏平均每天销售这种商品的利润w(元)与销售价x之间的函数关系式;
(2)当这种商品的销售价为多少元时,可以获得最大利润?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)由题意得,每天销售量与销售单价之间的关系可近似看作一次函数,利润=(定价-进价)×销售量,从而列出关系式;
(2)根据公式,求出x=20时W最大,进而得出答案.
(2)根据公式,求出x=20时W最大,进而得出答案.
解答:解:(1)由题意得出:
w=(x-10)×y,
=(x-10)•(-2x+60)
=-2x2+80x-600;
(2)∵w=-2x2+80x-600,
∴当x=-
=20时,w最大=-2×202+80×20-600=200(元).
答:当这种商品的销售价为20元时,可以获得最大利润,最大利润是200元.
w=(x-10)×y,
=(x-10)•(-2x+60)
=-2x2+80x-600;
(2)∵w=-2x2+80x-600,
∴当x=-
| b |
| 2a |
答:当这种商品的销售价为20元时,可以获得最大利润,最大利润是200元.
点评:此题考查了二次函数的性质及其应用,将实际问题转化为求函数最值问题,从而来解决实际问题.

练习册系列答案
相关题目
直角三角形两直角边长是6和8,则斜边上的高长( )
| A、4.8 | B、5 |
| C、10 | D、不能确定 |
下列各组图形中,成轴对称的两个图形是( )
A、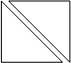 |
B、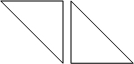 |
C、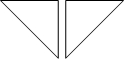 |
D、 |
 如图,把小圆形场地的半径增加5m得到大圆形场地,场地面积增加了一倍,则小圆形场地的半径=
如图,把小圆形场地的半径增加5m得到大圆形场地,场地面积增加了一倍,则小圆形场地的半径=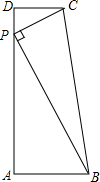 如图,在梯形ABCD中,AB∥DC,∠A=90°,点P在AD边上,且PC⊥PB.若AB=6,DC=4,
如图,在梯形ABCD中,AB∥DC,∠A=90°,点P在AD边上,且PC⊥PB.若AB=6,DC=4, 如图,网格中每个小正方形的边长均为1个单位长度,△ABC的三个顶点都在网格的格点上.
如图,网格中每个小正方形的边长均为1个单位长度,△ABC的三个顶点都在网格的格点上.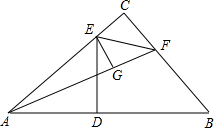 如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,垂足是D,F是BC上一点,EF平分∠AFC,EG⊥AF于点G.
如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于点E,垂足是D,F是BC上一点,EF平分∠AFC,EG⊥AF于点G.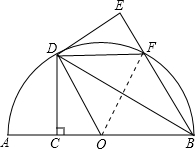 如图.AB是半圆O的直径,点C是半径OA上的点,过点C作CD⊥AB交半圆O于点D,将△BCD沿BD折叠得到△BED,BE交半圆O于点F,连接DF
如图.AB是半圆O的直径,点C是半径OA上的点,过点C作CD⊥AB交半圆O于点D,将△BCD沿BD折叠得到△BED,BE交半圆O于点F,连接DF