题目内容
如图，扇形AOB的圆心角为直角，正方形OCDE内接于扇形，点C，E，D分别在OA，OB，弧AB上，过点A作AF⊥ED，交ED的延长线于F，垂足为F，如果正方形的边长为1，那么阴影部分的面积为 ．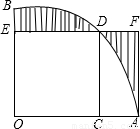
【答案】分析：通过观察图形可知DE=DC，BE=AC，弧BD=弧AD，阴影部分的面积正好等于长方形ACDF的面积，根据正方形的性质求出扇形的半径，从而求出AC的长，即可求出长方形ACDF的面积．
解答：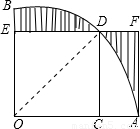
解：连接OD，
∵正方形的边长为1，即OC=CD=1，
∴OD=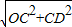
=
，
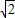∴AC=OA-OC=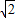
-1，
∵DE=DC，BE=AC，弧BD=弧AD
∴S阴=长方形ACDF的面积=AC•CD=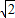
-1．
点评：本题要把不规则的图形通过几何变换转化为规则图形的面积求解．如通过观察可知阴影部分的面积正好等于长方形ACDF的面积，直接根据相关条件求长方形ACDF的面积即可．
解答：
解：连接OD，∵正方形的边长为1，即OC=CD=1，
∴OD=
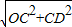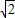=，∴AC=OA-OC=
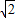-1，∵DE=DC，BE=AC，弧BD=弧AD
∴S阴=长方形ACDF的面积=AC•CD=
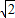-1．点评：本题要把不规则的图形通过几何变换转化为规则图形的面积求解．如通过观察可知阴影部分的面积正好等于长方形ACDF的面积，直接根据相关条件求长方形ACDF的面积即可．
练习册系列答案
计算高手系列答案
相关题目
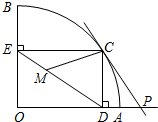如图，扇形OAB的半径OA=r，圆心角∠AOB=90°，点C是
（2012•珠海三模）如图：扇形OAB的圆心角∠AOB=120°，半径OA=6cm，
（1997•台湾）已知：如图，扇形AOB．求作：一个与OA、OB、
如图，扇形OAB的半径OA=r，圆心角∠AOB=90°，点C是
上异于A、B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，点M在DE上，DM=2EM，过点C的直线CP交OA的延长线于点P，且∠CPO=∠CDE．
r；