题目内容
在一列数a1，a2，a3…中，a2-a1=a3-a2=a4-a3=…=| 4 | 7 |
分析：观察这一列数，由已知得：a2-a1=
，a3-a2=
，a4-a3=
，…，a19-a18=
，则得：a2-a1+a3-a2+a4-a3+…+a19-a18=
×18，从而求出a19．
| 4 |
| 7 |
| 4 |
| 7 |
| 4 |
| 7 |
| 4 |
| 7 |
| 4 |
| 7 |
解答：解：由已知通过观察得：
：a2-a1=
，
a3-a2=
，
a4-a3=
，
…，
a19-a18=
，
则得：a2-a1+a3-a2+a4-a3+…+a19-a18=
×18，
所以得：a19=a1+
．
故答案为：a1+
．
：a2-a1=
| 4 |
| 7 |
a3-a2=
| 4 |
| 7 |
a4-a3=
| 4 |
| 7 |
…，
a19-a18=
| 4 |
| 7 |
则得：a2-a1+a3-a2+a4-a3+…+a19-a18=
| 4 |
| 7 |
所以得：a19=a1+
| 72 |
| 7 |
故答案为：a1+
| 72 |
| 7 |
点评：此题考查的知识点是数字变化类问题，解题的关键是由已知写成每个算式等于
，把每个等式的左边相加等于右边相加，求出答案．
| 4 |
| 7 |
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
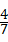，则a19= 
，则a19= ．