题目内容
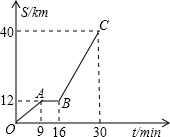 如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:(1)汽车在前9分钟内的平均速度是
| 4 |
| 3 |
| 4 |
| 3 |
(2)汽车在中途停了多长时间?
7min
7min
(3)求OA与BC的函数关系式,并写出自变量t的取值范围.
分析:(1)根据速度=路程÷时间,列式计算即可得解;
(2)根据停车时路程没有变化列式计算即可;
(3)利用待定系数法求一次函数解析式解答即可.
(2)根据停车时路程没有变化列式计算即可;
(3)利用待定系数法求一次函数解析式解答即可.
解答:解:(1)平均速度=
=
km/min;
(2)从9分到16分,路程没有变化,为停车时间,
16-9=7min.
(3)设OA的函数关系式为S=kt,
∵点A的坐标为(9,12),
∴9k=12,
解得k=
,
所以,OA的函数关系式为S=
t(0≤t≤9);
设BC的函数关系式为S=kt+b,
∵点B(16,12),C(30,40),
∴
,
解得
,
所以,BC的函数关系式为S=2t-20(16≤t≤30).
故答案为:(1)
km/min;(2)7min.
| 12 |
| 9 |
| 4 |
| 3 |
(2)从9分到16分,路程没有变化,为停车时间,
16-9=7min.
(3)设OA的函数关系式为S=kt,
∵点A的坐标为(9,12),
∴9k=12,
解得k=
| 4 |
| 3 |
所以,OA的函数关系式为S=
| 4 |
| 3 |
设BC的函数关系式为S=kt+b,
∵点B(16,12),C(30,40),
∴
|
解得
|
所以,BC的函数关系式为S=2t-20(16≤t≤30).
故答案为:(1)
| 4 |
| 3 |
点评:本题考查了一次函数的应用,待定系数法求函数解析式,比较简单,准确识图并获取信息是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知某型汽车在干燥的路面上,汽车停止行驶所需的刹车距离与刹车时的车速之间有下表所示的对应关系.
| 速度v(km/h) | 48 | 64 | 80 | 96 | 112 | … |
| 刹车距离s(m) | 22.5 | 36 | 52.5 | 72 | 94.5 | … |
(1)请你以汽车刹车时的车速为v为自变量,刹车距离s为函数,在如图26-3-7所示的坐标系中描点连线,画出函数的图象;
(2)观察所画的函数的图象,你发现了什么?
(3)若把这个函数的图象看成是一条抛物线,请根据表中所给的数据,选择三对,求出它的函数关系式;
(4)用你留下的两对数据,验证一下你所得到的结论是否正确.
已知某型汽车在干燥的路面上,汽车停止行驶所需的刹车距离与刹车时的车速之间有下表所示的对应关系.
| 速度v(km/h) | 48 | 64 | 80 | 96 | 112 | … |
| 刹车距离s(m) | 22.5 | 36 | 52.5 | 72 | 94.5 | … |
(1)请你以汽车刹车时的车速为v为自变量,刹车距离s为函数,在如图26-3-7所示的坐标系中描点连线,画出函数的图象;
(2)观察所画的函数的图象,你发现了什么?
(3)若把这个函数的图象看成是一条抛物线,请根据表中所给的数据,选择三对,求出它的函数关系式;
(4)用你留下的两对数据,验证一下你所得到的结论是否正确.