题目内容
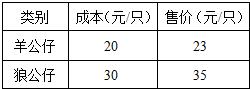
动画片《喜羊羊与灰太狼》正在热播中．某企业获得了生产羊公仔和狼公仔的专利．为了满足市场需求，该企业现在开始生产羊和狼两种类别的公仔，每天共生产450只；两种公仔成本和售价如下表所示，设每天生产羊公仔x只，共获利y元．
（1）求出y与x之间的函数关系式；
（2）如果该企业每天投入成本不超过10000元，那么每天要获利最多，应生产羊公仔和狼公仔各多少只？
（1）求出y与x之间的函数关系式；
（2）如果该企业每天投入成本不超过10000元，那么每天要获利最多，应生产羊公仔和狼公仔各多少只？
| 类别 | 成本（元/只） | 售价（元/只） |
| 羊公仔 | 20 | 23 |
| 狼公仔 | 30 | 35 |
（1）由题意可知：y=（23-20）x+（35-30）（450-x）
整理得：y=-2x+2250；
（2）由20x+30（450-x）≤10000，得x≥350
根据（1）中的函数关系式：y=-2x+2250；可知，x越大，y越小．
∴当x=350时，y有最大值为1550．
答：每天应该生产羊公仔350个，狼公仔100个．
整理得：y=-2x+2250；
（2）由20x+30（450-x）≤10000，得x≥350
根据（1）中的函数关系式：y=-2x+2250；可知，x越大，y越小．
∴当x=350时，y有最大值为1550．
答：每天应该生产羊公仔350个，狼公仔100个．
练习册系列答案
小学教材全测系列答案
相关题目
