题目内容
(11·钦州)(本题满分9分)
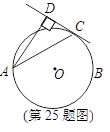
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:AC平分∠DAB;
(2)过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
(3)若CD=4,AC=4 ,求垂线段OE的长.
,求垂线段OE的长.
解:(1)连接OC
∵CD切⊙O于点C,
∴OC⊥CD
又∵AD⊥CD
∴OC∥AD
∴∠OCA=∠DAC
∵OC=OA
∴∠OCA=∠OAC
∴∠OAC=∠DAC

∴AC平分∠DAB ………………3分
(2)解:点O作线段AC的垂线OE如图所示
(3)解:在Rt△ACD中,CD=4,AC=4 ,
,
 ………………6分
………………6分
∵OE⊥AC

即垂线段OE的长为 ………………9分
………………9分
【解析】略

(11·钦州)(本题满分9分)
某校为了解九年级800名学生的体育综合素质,随机抽查了50名学生进行体育综合测试,所得成绩整理分成五组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
频数分布表 扇形统计图
| 组别 | 成绩(分) | 频数 |
| A | 50≤x<60 | 3 |
| B | 60≤x<80 | m |
| C | 70≤x<80 | 10 |
| D | 80≤x<90 | n |
| E | 90≤x<100 | 15 |
(1)频数分布表中的m=_ ▲ ,n=_ ▲ ;
(2)样本中位数所在成绩的级别是_ ▲ ,扇形统计图中,E组所对应的扇形圆心角的度数是_ ▲ ;
(3)请你估计该校九年级的学生中,体育综合测试成绩不少于80分的大约有多少人?