题目内容
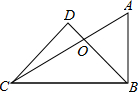
 将一副三角尺按如图方式叠在一起,三角尺的3个角的顶点是A、C、D,记作“三角尺ACD”;三角尺的3个角的顶点是E、C、B,记作“三角尺ECB”,且∠ACD=∠ECB=90°,∠A=60°,∠D=30°,∠E=∠B=45°.
将一副三角尺按如图方式叠在一起,三角尺的3个角的顶点是A、C、D,记作“三角尺ACD”;三角尺的3个角的顶点是E、C、B,记作“三角尺ECB”,且∠ACD=∠ECB=90°,∠A=60°,∠D=30°,∠E=∠B=45°.(1)若∠ACB=140°,求∠DCE的度数;
(2)比较∠ACE与∠DCB的大小,并说明理由;
(3)三角尺ACD不动,将三角尺BCE的CE边与CA边重合,然后绕点C按顺时针方向任意转动一个角度,当∠ACE等于多少度时(0°<∠ACE<90°),这两块三角尺各有一条边所在的直线互相垂直,请直接写出∠ACE所有可能的值,不必说明理由.(提示:三角形内角和为180°.)
分析:(1)求出∠ECA度数,得出∠DCE=90°-∠ACE,代入求出即可;
(2)根据∠ACD=∠ECB=90°,都减去∠ECD,即可得出答案;
(3)30°时CE⊥AD,45°时BE⊥CD,75°时BE⊥AD.
(2)根据∠ACD=∠ECB=90°,都减去∠ECD,即可得出答案;
(3)30°时CE⊥AD,45°时BE⊥CD,75°时BE⊥AD.
解答:解:(1)∵∠ACB=140°,∠ECB=90°,
∴∠ECA=140°-90°=50°,
∵∠ACD=90°,
∴∠DCE=90°-50°=40°;
(2)∠ACE=∠BCD,
理由是:∵∠ACD=∠ECB=90°,
∴∠ACD-∠ECD=∠ECB-∠ECD,
∴∠ACE=∠BCD;
(3)可以是30°,45°,75°.
∴∠ECA=140°-90°=50°,
∵∠ACD=90°,
∴∠DCE=90°-50°=40°;
(2)∠ACE=∠BCD,
理由是:∵∠ACD=∠ECB=90°,
∴∠ACD-∠ECD=∠ECB-∠ECD,
∴∠ACE=∠BCD;
(3)可以是30°,45°,75°.
点评:本题考查了角的有关计算,难点是理解关于重叠问题.

练习册系列答案
相关题目
 (2006•福州质检)将一副三角尺按如图的位置摆放,则∠BOC的度数是
(2006•福州质检)将一副三角尺按如图的位置摆放,则∠BOC的度数是 将一副三角板按如图方式摆放,则图中不存在的角度是( )
将一副三角板按如图方式摆放,则图中不存在的角度是( )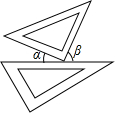 如图,将一副三角尺按如图所示方式摆放,则图中∠α与∠β的关系是
如图,将一副三角尺按如图所示方式摆放,则图中∠α与∠β的关系是 将一副三角尺按如图方式叠在一起,三角尺的3个角的顶点是A、C、D,记作“三角尺ACD”;三角尺的3个角的顶点是E、C、B,记作“三角尺ECB”,且∠ACD=∠ECB=90°,∠A=60°,∠D=30°,∠E=∠B=45°.
将一副三角尺按如图方式叠在一起,三角尺的3个角的顶点是A、C、D,记作“三角尺ACD”;三角尺的3个角的顶点是E、C、B,记作“三角尺ECB”,且∠ACD=∠ECB=90°,∠A=60°,∠D=30°,∠E=∠B=45°.