Question

【题目】如图，在△ABC中，BC=1，点P1 ， M1分别是AB，AC边的中点，点P2 ， M2分别是AP1 ， AM1的中点，点P3 ， M3分别是AP2 ， AM2的中点，按这样的规律下去，PnMn的长为（n为正整数）．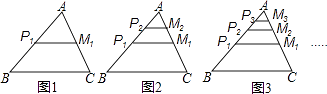

Answer 1

【答案】
【解析】解：在△ABC中，BC=1，点P1，M1分别是AB，AC边的中点，点P2，M2分别是AP1，AM1的中点，点P3，M3分别是AP2，AM2的中点，

可得：P1M1= ，P2M2= ，故PnMn= ，

所以答案是：

【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．