题目内容
(1)如图中①、②,锐角的正弦值和余弦值都是随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值及余弦值的变化规律;(2)根据你探索到的规律,试分别比较18°、34°、50°、62°、88°这些锐角的正弦值的大小和余弦值的大小.
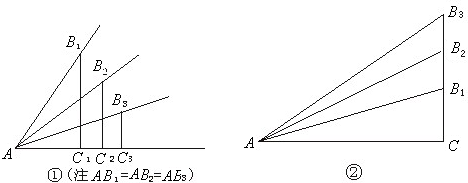
分析:(1)根据概念,不难发现:随着一个锐角的增大,它的对边在减小,邻边在增大,即可找到正余弦值的变化规律;
(2)根据正余弦值的变化规律,即可比较正余弦值的大小.
(2)根据正余弦值的变化规律,即可比较正余弦值的大小.
解答:解:(1)由图①,知
sin∠B1AC1=
,sin∠B2AC2=
,
sin∠B3AC3=
.
∵AB1=AB2=AB3且B1C1>B2C2>B3C3,
∴
>
>
.
∴sin∠B1AC1>sin∠B2AC2>sin∠B3AC3.
而∠B1AC1>∠B2AC2>∠B3AC3,
而对于cos∠B1AC1=
,
cos∠B2AC2=
,
cos∠B3AC3=
.
∵AC1<AC2<AC3,
∴cos∠B1AC1<cos∠B2AC2<cos∠B3AC3.
而∠B1AC1>∠B2AC2>∠B3AC3.
由图②知sin∠B3AC=
,
∴sin2∠B3AC=
.
∴1-sin2∠B3AC=1-
=
=
.
同理,sin∠B2AC=
,1-sin2∠B2AC=
,
sin∠B1AC=
,1-sin2∠B1AC=
.
∵AB3>AB2>AB1,∴
<
<
.
∴1-sin2∠B3AC<1-sin2∠B2AC<1-sin2∠B1AC.
∴sin2∠B3AC>sin2∠B2AC>sin2∠B1AC.
∵∠B3AC,∠B2AC,∠B1AC均为锐角,
∴sin∠B3AC>sin∠B2AC>sin∠B1AC.
而∠B3AC>∠B2AC>∠B1AC.
而对于cos∠B3AC=
,
cos∠B2AC=
,
cos∠B1AC=
.
∵AB3>AB2>AB1,∴
<
<
.
∴cos∠B3AC<cos∠B2AC<cos∠B1AC.
而∠B3AC>∠B2AC>∠B1AC.
结论:锐角的正弦值随角度的增大而增大,锐角的余弦值随角度的增大而减小.
(2)由(1)知
sin18°<sin34°<sin50°<sin62°<sin88°,
cos18°>cos34°>cos50°>cos62°>cos88°.
sin∠B1AC1=
| B1C1 |
| AB1 |
| B2C2 |
| AB2 |
sin∠B3AC3=
| B3C3 |
| AB3 |
∵AB1=AB2=AB3且B1C1>B2C2>B3C3,
∴
| B1C1 |
| AB1 |
| B2C2 |
| AB2 |
| B3C3 |
| AB3 |
∴sin∠B1AC1>sin∠B2AC2>sin∠B3AC3.
而∠B1AC1>∠B2AC2>∠B3AC3,
而对于cos∠B1AC1=
| AC1 |
| AB1 |
cos∠B2AC2=
| AC2 |
| AB2 |
cos∠B3AC3=
| AC3 |
| AB3 |
∵AC1<AC2<AC3,
∴cos∠B1AC1<cos∠B2AC2<cos∠B3AC3.
而∠B1AC1>∠B2AC2>∠B3AC3.
由图②知sin∠B3AC=
| B3C |
| AB3 |
∴sin2∠B3AC=
| B3C2 | ||
A
|
∴1-sin2∠B3AC=1-
| B3C2 | ||
A
|
A
| ||
A
|
| AC2 | ||
A
|
同理,sin∠B2AC=
| B2C |
| AB2 |
| AC2 | ||
A
|
sin∠B1AC=
| B1C |
| AB2 |
| AC2 | ||
A
|
∵AB3>AB2>AB1,∴
| AC2 | ||
A
|
| AC2 | ||
A
|
| AC2 | ||
A
|
∴1-sin2∠B3AC<1-sin2∠B2AC<1-sin2∠B1AC.
∴sin2∠B3AC>sin2∠B2AC>sin2∠B1AC.
∵∠B3AC,∠B2AC,∠B1AC均为锐角,
∴sin∠B3AC>sin∠B2AC>sin∠B1AC.
而∠B3AC>∠B2AC>∠B1AC.
而对于cos∠B3AC=
| AC |
| AB3 |
cos∠B2AC=
| AC |
| AB2 |
cos∠B1AC=
| AC |
| AB1 |
∵AB3>AB2>AB1,∴
| AC |
| AB3 |
| AC |
| AB2 |
| AC |
| AB1 |
∴cos∠B3AC<cos∠B2AC<cos∠B1AC.
而∠B3AC>∠B2AC>∠B1AC.
结论:锐角的正弦值随角度的增大而增大,锐角的余弦值随角度的增大而减小.
(2)由(1)知
sin18°<sin34°<sin50°<sin62°<sin88°,
cos18°>cos34°>cos50°>cos62°>cos88°.
点评:理解锐角三角函数的概念,掌握锐角三角函数值的变化规律.

练习册系列答案
相关题目
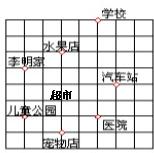 21、请你在如图中建立直角坐标系,使汽车站的坐标是(3,1),并用坐标说明儿童公园和学校的位置,此时宠物店在汽车站的什么方向线上?
21、请你在如图中建立直角坐标系,使汽车站的坐标是(3,1),并用坐标说明儿童公园和学校的位置,此时宠物店在汽车站的什么方向线上? 6、如图中是一球吊在空中,当发光的手电筒由远及近时,落在竖直墙面上的球影子会
6、如图中是一球吊在空中,当发光的手电筒由远及近时,落在竖直墙面上的球影子会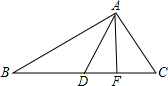 如图中,∠B=36°,∠C=76°,AD、AF分别是△ABC的角平分线和高,则∠DAF=
如图中,∠B=36°,∠C=76°,AD、AF分别是△ABC的角平分线和高,则∠DAF=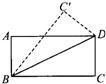 26、如图中的△BDC′是将矩形纸片ABCD沿对角线BD折叠到的.则图中(包括虚,实线)共有
26、如图中的△BDC′是将矩形纸片ABCD沿对角线BD折叠到的.则图中(包括虚,实线)共有 24、茅坪民族中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后回到C处,请你在下图帮助他设计一条行走路线,使其所走的总路程最短?
24、茅坪民族中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后回到C处,请你在下图帮助他设计一条行走路线,使其所走的总路程最短?