题目内容
(2007•常德)某化工厂现有甲种原料7吨,乙种原料5吨,现计划用这两种原料生产两种不同的化工产品A和B共8吨,已知生产每吨A,B产品所需的甲、乙两种原料如下表:| 甲原料 | 乙原料 | |
| A产品 | 0.6吨 | 0.8吨 |
| B产品 | 1.1吨 | 0.4吨 |
(1)求y与x的函数关系式,并求出x的取值范围;
(2)问化工厂生产A产品多少吨时,所获得的利润最大?最大利润是多少?
【答案】分析:(1)求函数关系式不难.求x的取值范围要考虑甲乙两种原材料的数量.
(2)因为利润与产品A的关系式已求出,根据函数性质,结合自变量的取值范围即可求出函数的最值.
解答:解:(1)据题意得:
y=0.45x+(8-x)×0.5=-0.05x+4,
因为生产两种产品所需的甲种原料为:0.6x+1.1×(8-x),
所需的乙种原料为:0.8x+0.4×(8-x),
则可得不等式组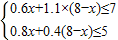 ,
,
解得3.6≤x≤4.5;
(2)因为函数关系式y=-0.05x+4中的-0.05<0,
所以y随x的增大而减小.
则由(1)可知当x=3.6时,y取最大值,且为3.82万元.
答:化工厂生产A产品3.6吨时,所获得的利润最大,最大利润是3.82万元.
点评:此题为一次函数的综合应用,有一定难度.求自变量的取值范围涉及到解不等式组;求最值要根据性质结合自变量的取值范围求解.
(2)因为利润与产品A的关系式已求出,根据函数性质,结合自变量的取值范围即可求出函数的最值.
解答:解:(1)据题意得:
y=0.45x+(8-x)×0.5=-0.05x+4,
因为生产两种产品所需的甲种原料为:0.6x+1.1×(8-x),
所需的乙种原料为:0.8x+0.4×(8-x),
则可得不等式组
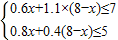 ,
,解得3.6≤x≤4.5;
(2)因为函数关系式y=-0.05x+4中的-0.05<0,
所以y随x的增大而减小.
则由(1)可知当x=3.6时,y取最大值,且为3.82万元.
答:化工厂生产A产品3.6吨时,所获得的利润最大,最大利润是3.82万元.
点评:此题为一次函数的综合应用,有一定难度.求自变量的取值范围涉及到解不等式组;求最值要根据性质结合自变量的取值范围求解.

练习册系列答案
相关题目
(2007•常德)某化工厂现有甲种原料7吨,乙种原料5吨,现计划用这两种原料生产两种不同的化工产品A和B共8吨,已知生产每吨A,B产品所需的甲、乙两种原料如下表:
销售A,B两种产品获得的利润分别为0.45万元/吨、0.5万元/吨.若设化工厂生产A产品x吨,且销售这两种产品所获得的总利润为y万元.
(1)求y与x的函数关系式,并求出x的取值范围;
(2)问化工厂生产A产品多少吨时,所获得的利润最大?最大利润是多少?
| 甲原料 | 乙原料 | |
| A产品 | 0.6吨 | 0.8吨 |
| B产品 | 1.1吨 | 0.4吨 |
(1)求y与x的函数关系式,并求出x的取值范围;
(2)问化工厂生产A产品多少吨时,所获得的利润最大?最大利润是多少?
(2007•常德)阅读理解:市盈率是某种股票每股市价与每股盈利的比率(即:某支股票的市盈率=该股票当前每股市价÷该股票上一年每股盈利).市盈率是估计股票价值的最基本、最重要的指标之一.一般认为该比率保持在30以下是正常的,风险小,值得购买;过大则说明股价高,风险大,购买时应谨慎.
应用:某日一股民通过互联网了解到如下三方面的信息:
①甲股票当日每股市价与上年每股盈利分别为5元、0.2元
乙股票当日每股市价与上年每股股盈利分别为8元、0.01元
②该股民所购买的15支股票的市盈率情况如下表:
③丙股票最近10天的市盈率依次为:
20 20 30 28 32 35 38 42 40 44
根据以上信息,解答下列问题:
(1)甲、乙两支股票的市盈率分别是多少?
(2)该股民所购买的15支股票中风险较小的有几支?
(3)求该股民所购15支股票的市盈率的平均数、中位数与众数;
(4)请根据丙股票最近10天的市盈率画出折线统计图,并依据市盈率的有关知识和折线统计图,就丙股票给该股民一个合理的建议.

应用:某日一股民通过互联网了解到如下三方面的信息:
①甲股票当日每股市价与上年每股盈利分别为5元、0.2元
乙股票当日每股市价与上年每股股盈利分别为8元、0.01元
②该股民所购买的15支股票的市盈率情况如下表:
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 市盈率 | 25 | 800 | 61 | 19 | 18 | 28 | 28 | 35 | 59 | 80 | 62 | 80 | 80 | 82 | 43 |
20 20 30 28 32 35 38 42 40 44
根据以上信息,解答下列问题:
(1)甲、乙两支股票的市盈率分别是多少?
(2)该股民所购买的15支股票中风险较小的有几支?
(3)求该股民所购15支股票的市盈率的平均数、中位数与众数;
(4)请根据丙股票最近10天的市盈率画出折线统计图,并依据市盈率的有关知识和折线统计图,就丙股票给该股民一个合理的建议.