��Ŀ����
����Ŀ������������a��b��c��M![]() ��ʾa��b��c����������ƽ������min
��ʾa��b��c����������ƽ������min![]() ��ʾa��b��c������������С�������磺
��ʾa��b��c������������С�������磺
M![]() ��min
��min![]() ����1��
����1��
M![]() ��min
��min![]() ��
��![]() ��
��
����������⣺
(1) ��գ�min�� a, a-1, a+2 ����______________��
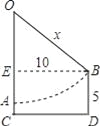
(2) ��min![]() ��2����x��ȡֵ��Χ��______________��
��2����x��ȡֵ��Χ��______________��
(3) ����M![]() ��min
��min![]() ����ôx��______________��
����ôx��______________��
�ڸ��ݢ٣��㷢�ֽ�������M![]() ��min
��min![]() ����______________������a��b��c�Ĵ�С��ϵ����
����______________������a��b��c�Ĵ�С��ϵ����
�����âڽ�����⣺(д�����Ĺ���)
��M![]() ��min
��min![]() ��
��
��x��y ��ֵ.
���𰸡� a-1 0��x��1 ��1 ��a��b��c��x+y=-4��
�������������������1���ȱȽ�a, a-1, a+2�Ĵ�С���ٸ���������ɵó��𰸣�
��2���ȸ�����������г�����ʽ�飬�ٽ�����⼴�ɵó��𰸣�
��3���������й涨��M{a��b��c}��ʾ����������ƽ������min{a��b��c}��ʾa��b��c���������е���С�����г������鼴����⣮
�⣺��1����a-1<a<a+2��
��min�� a, a-1, a+2 ����a-1��
��2��������ã�
![]() ��
��
��ã�0��x��1��
��3����M{2��x+1��2x}=![]() =x+1=min{2��x+1��2x}��
=x+1=min{2��x+1��2x}��
��![]() ��
��
��![]() ��
��
��x=1��
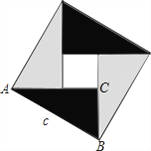
����M{a��b��c}=min{a��b��c}����a=b=c��
�۸��ݢڵã�2x+y+2=x+2y=2x-y��
��ã�x=-3��y=-1��
��x+y=-4��

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�