Question

一个容器由上、下竖直放置的两个圆柱体A，B连接而成．向该容器内匀速注水，容器内水面的高度h（厘米）与注水时间t（分）的函数关系如图所示．若上面A圆柱体的底面积是300平方厘米，下面圆柱体B的底面积是500平方厘米，则每分钟向容器内注水     立方厘米．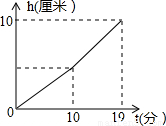

Answer 1

【答案】分析：设圆柱体B的高为h厘米，注水速度为v厘米³/分钟，从而结合图象可用h表示出v，然后再由9分钟后容器内水位上升（10-h）厘米，可得出方程，解出即可得出答案．
解答：解：设圆柱体B的高为h厘米，注水速度为v厘米³/分钟，
由题意得，10v=500h，
则v=50h，
∵9分钟后容器内水位上升（10-h）厘米，
∴50h×9=300（10-h），
解得：h=4，
故可得v=50h=200厘米³/分钟．
故答案为：200．
点评：本题考查了数学知识的实际应用，解答本题的关键是设出未知数，利用两个圆柱体水位的上升得出方程，有一定难度．