题目内容
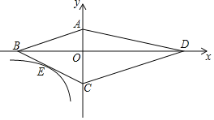
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 位于对称轴的左侧),与
位于对称轴的左侧),与![]() 轴交于点
轴交于点![]() .点
.点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作直线
作直线![]() 轴交图象于点
轴交图象于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() .
.
(1)求该二次函数的对称轴及![]() 的值.
的值.
(2)将顶点![]() 向右平移
向右平移![]() 个单位至点
个单位至点![]() ,再过点
,再过点![]() 作直线
作直线![]() 的对称点
的对称点![]() ,若点
,若点![]() 在
在![]() 轴上方的图象上一点且到
轴上方的图象上一点且到![]() 轴距离为1,求
轴距离为1,求![]() ,
,![]() 的值.
的值.
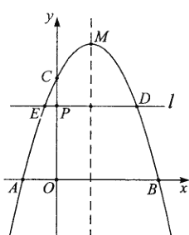
【答案】(1)直线![]() ;
;![]() ;(2)
;(2)![]()
【解析】
(1)由![]() ,即可得到对称轴,然后求出a的值即可;
,即可得到对称轴,然后求出a的值即可;
(2)先求出顶点坐标,然后根据平移的性质和轴对称的性质,得到点![]() 的坐标,再结合题意,列出等式,即可求出答案.
的坐标,再结合题意,列出等式,即可求出答案.
(1)解:如图,设直线![]() 与对称轴交于点
与对称轴交于点![]() ,
,
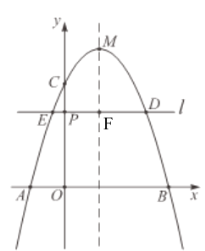
∵![]() .
.
∴![]() ,即对称轴为:直线
,即对称轴为:直线![]() .
.
∴![]() ;
;
∴对称轴为直线![]() ,
,![]() 的值为
的值为![]() .
.
(2)解:由(1)知:![]()
∴![]() ,将
,将![]() 向右平移
向右平移![]() 个单位至点
个单位至点![]()
∴![]() ,从而关于直线
,从而关于直线![]() 的对称点
的对称点![]() .
.
又∵点![]() 在
在![]() 轴上方抛物线上一点且到
轴上方抛物线上一点且到![]() 轴距离为1
轴距离为1
∴![]() ,再将
,再将![]() 代入抛物线得:
代入抛物线得:
![]() ,
,![]() (舍),
(舍),
综上可知,![]() .
.

【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
【题目】某校开展“文明在行动”的志愿者活动,准备购买某一品牌书包送到希望学校.在![]() 商店,无论一次购买多少,价格均为每个50元.在
商店,无论一次购买多少,价格均为每个50元.在![]() 商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
(Ⅰ)根据题意填表:
一次购买数量/个 | 5 | 10 | 15 | … |
| 500 | … | ||
| 600 | … |
(Ⅱ)设在![]() 商店花费
商店花费![]() 元,在
元,在![]() 商店花费
商店花费![]() 元,分别求出
元,分别求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空;
①若小丽在![]() 商店和在
商店和在![]() 商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
②若小丽在同一商店一次购买书包的数量为50个,则她在![]() 两个商店中的______商店购买花费少;
两个商店中的______商店购买花费少;
③若小丽在同一商店一次购买书包花费了1800元,则她在![]() 两个商店中_______商店购买数量多.
两个商店中_______商店购买数量多.