题目内容
【题目】如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD,BC分别交于点E,F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.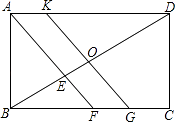
(1)求证:△DOK≌△BOG;
(2)探究线段AB、AK、BG三者之间的关系,并证明你的结论;
(3)若KD=KG,BC=2 ![]() ﹣1,求KD的长度.
﹣1,求KD的长度.
【答案】
(1)证明:∵在矩形ABCD中,AD∥BC,
∴∠KDO=∠GBO,∠DKO=BGO.
∵点O是BD的中点;
∴DO=BO.
在△DOK和△BOG中, 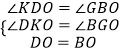
∴△DOK≌△BOG(AAS).
(2)解:AB+AK=BG;证明如下:
∵四边形ABCD是矩形;
∴∠BAD=∠ABC=90°,AD∥BC.
又∵AF平分∠BAD,
∴∠BAF=∠BFA=45°.
∴AB=BF.
∵OK∥AF,AK∥FG,
∴四边形AFGK是平行四边形.
∴AK=FG.
∵BG=BF+FG;
∴BG=AB+AK.
(3)解:∵四边形AFGK是平行四边形.
∴AK=FG,AF=KG
又∵△DOK≌△BOG,且KD=KG,
∴AF=KG=KD=BG.
设AB=a,则AF=KG=KD=BG= ![]() a.
a.
∴AK=2 ![]() ﹣1﹣
﹣1﹣ ![]() a,FG=BG﹣BF=
a,FG=BG﹣BF= ![]() a﹣a.
a﹣a.
∴2 ![]() ﹣1﹣
﹣1﹣ ![]() a=
a= ![]() a﹣a.
a﹣a.
解得a=1.
∴KD= ![]() a=
a= ![]() .
.
【解析】(1)在矩形ABCD中,AD∥BC,得到∠KDO=∠GBO,∠DKO=BGO,DO=BO,得到△DOK≌△BOG(AAS);(2)四边形ABCD是矩形,得到∠BAD=∠ABC=90°,AD∥BC,又AF平分∠BAD,得到∠BAF=∠BFA=45°,AB=BF,由OK∥AF,AK∥FG,得到四边形AFGK是平行四边形,得到AK=FG,BG=BF+FG,即BG=AB+AK;(3)四边形AFGK是平行四边形,得到AK=FG,AF=KG,又△DOK≌△BOG,且KD=KG,得到AF=KG=KD=BG,设AB=a,则AF=KG=KD=BG=![]() a,得到AK=2
a,得到AK=2![]() ﹣1-
﹣1-![]() a,FG=BG﹣BF=
a,FG=BG﹣BF=![]() a﹣a,解得a=1,得到KD=
a﹣a,解得a=1,得到KD=![]() a=
a=![]() .
.