Question

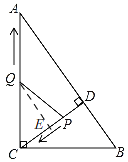
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

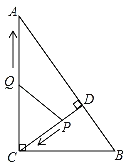
（1）求线段CD的长；

（2）当t为何值时，△CPQ与△ABC相似？

（3）是否存在某一时刻，使得PQ分△ACD的面积为2：3？若存在，求出t的值，若不存在，请说明理由．

Answer 1

【答案】（1）CD＝；（2）t为3秒或秒时，△CPQ与△ABC相似；（3）不存在，见解析.

【解析】

（1）先利用勾股定理求出AB＝10，进利用面积法求出CD；

（2）先表示出CP，再判断出∠ACD＝∠B，进而分两种情况，利用相似三角形得出比例式建立方程求解，即可得出结论；

（3）先判断出△CEQ∽△CDA，得出，进而表示出QE＝t，再分当S△CPQ＝S△ACD时，和当S△CPD＝S△ACD时，利用面积建立方程求解即可得出结论．

解：（1）在Rt△ABC中，根据勾股定理得，AB＝＝＝10，

∵S△ABC＝ACBC＝ABCD，

∴CD＝＝＝，

（2）由（1）知，CD＝，

由运动知，CQ＝t，DP＝t，

∴CP＝CD﹣DP＝﹣t，

∵∠ACB＝90°，

∴∠ACD+∠BCD＝90°，

∵CD⊥AB，

∴∠B+∠BCD＝90°，

∴∠ACD＝∠B，

∵△CPQ与△ABC相似，

∴①△CPQ∽△BCA，

∴，

∴，

∴t＝3

②△CPQ∽△BAC，

∴，

∴

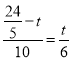
∴t＝，

即：t为3秒或秒时，△CPQ与△ABC相似；

（3）假设存在，如图，

在Rt△ACD中，根据勾股定理得，AD＝＝＝，

过点Q作CE⊥CD于E，

∴QE∥AD，

∴△CEQ∽△CDA，

∴，

∴，

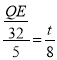∴QE＝t，

∵S△CPQ＝CPQE＝（﹣t）t，

∴S△ACD＝ADCD＝××，

∵PQ分△ACD的面积为2：3，

∴①当S△CPQ＝S△ACD时，

∴（﹣t）t＝×××，

∴25t2﹣120t+384＝0而△＝1202﹣4×25×384＝14400﹣38400＜0，

此方程无解，即：此种情况不存在，

②当S△CPD＝S△ACD时，（﹣t）t＝×××，

∴25t2﹣120t+576＝0，而△＝1202﹣4×25×576＝14400﹣57600＜0，

此方程无解，即：此种情况不存在，

即：不存在某时刻，使得PQ分△ACD的面积为2：3．