题目内容
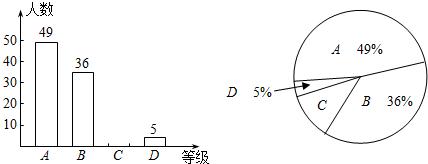
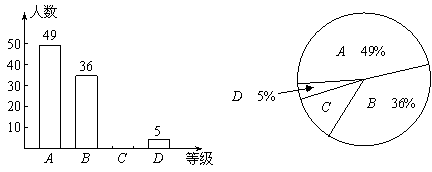
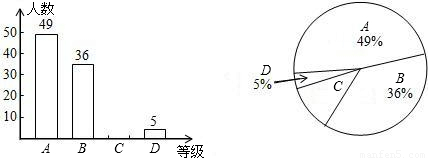
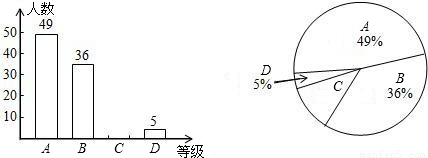
近来,校园安全问题引起了社会的极大关注,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列统计图(说明:A级:90分-100分;B级:75分-89分;C级:60分-74分;D级:60分以下).请结合图中提供的信息,解答下列问题:
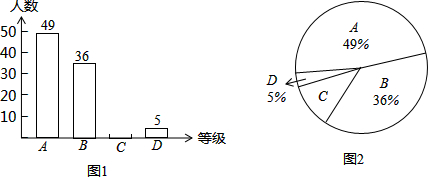
(1)请把条形统计图1补充完整;
(2)样本中C级的学生人数占抽样学生人数的百分比是
(3)扇形统计图2中C级所在的扇形的圆心角度数是
(4)如果从中选取5人,其中男生2人,女生人.现在打算从中随机选出两人,请用列表或画树形图的方法,求出所选两人恰好是一名男生和一名女生的概率.

(1)请把条形统计图1补充完整;
(2)样本中C级的学生人数占抽样学生人数的百分比是
10%
10%
;(3)扇形统计图2中C级所在的扇形的圆心角度数是
36°
36°
;(4)如果从中选取5人,其中男生2人,女生人.现在打算从中随机选出两人,请用列表或画树形图的方法,求出所选两人恰好是一名男生和一名女生的概率.
分析:(1)由等级A的人数除以所占的百分比求出样本的学生数,进而确定出等级C的学生数,补全图1即可;
(2)由扇形统计图中等级A,B,D的百分比求出等级C的百分比即可;
(3)由图2等级C的百分比乘以360即可得到结果;
(4)列表得出所有等可能的情况数,找出一男一女的情况数,即可求出所求的概率.
(2)由扇形统计图中等级A,B,D的百分比求出等级C的百分比即可;
(3)由图2等级C的百分比乘以360即可得到结果;
(4)列表得出所有等可能的情况数,找出一男一女的情况数,即可求出所求的概率.
解答:解:(1)样本中的学生数为49÷49%=100(人),
则等级C的人数为100-(49+36+5)=10(人),补全条形统计图,如图所示:

(2)等级C所占的百分比为1-(49%+5%+36%)=10%;
(3)扇形统计图2中C级所在的扇形的圆心角度数是360°×10%=36°;
(4)列表得:
所有等可能的情况有20种,其中一男一女的情况有12种,
则P(一男一女)=
=
.
故答案为:(2)10%;(3)36°
则等级C的人数为100-(49+36+5)=10(人),补全条形统计图,如图所示:

(2)等级C所占的百分比为1-(49%+5%+36%)=10%;
(3)扇形统计图2中C级所在的扇形的圆心角度数是360°×10%=36°;
(4)列表得:
| 男 | 男 | 女 | 女 | 女 | |
| 男 | --- | (男,男) | (男,女) | (男,女) | (男,女) |
| 男 | (男,男) | --- | (男,女) | (男,女) | (男,女) |
| 女 | (女,男) | (女,男) | --- | (女,女) | (女,女) |
| 女 | (女,男) | (女,男) | (女,女) | --- | (女,女) |
| 女 | (女,男) | (女,男) | (女,女) | (女,女) | --- |
则P(一男一女)=
| 12 |
| 20 |
| 3 |
| 5 |
故答案为:(2)10%;(3)36°
点评:此题考查了条形统计图,扇形统计图,以及列表法与树状图法,弄清题意是解本题的关键.

练习册系列答案
相关题目