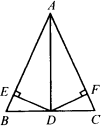
题目内容
已知:如图AD是△ABC的角平分线,E、F分别边AB、AC的中点,连接DE、DF,在不再连接其他线段的前提下,要使四边形AEDF成为菱形,还需添加一个什么条件?并证明四边形AEDF是菱形.
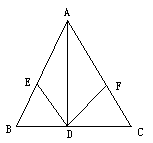
答案:
解析:
解析:
|
AB=AC(或∠B=∠C) 证明:∵AB=AC ∴AD平分∠BAC ∴D为BC中点 ∵E为AB中点 ∴DE为△ABC中位线 ∴DE∥AC,同理DF∥AB ∴四边形AEDF是平行四边形 ∵E、F分别为AB、AC中点 ∴AE= 又∵AB=AC ∴AE=AF ∴ 点评:题中的现有条件不能够推证出菱形AEDF,由结论入手要得菱形AEDF,首先想到能否得到平行四边形,只有D为BC中点即可,根据“AD是角平分线”联想到“三线合一”,因此可试加“AB=AC”,构造“等腰三角形三线合一”. |

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 18、已知:如图⊙O是Rt△CDE的外接圆,BC⊥CE,BD和CE的延长线交于点A,且OB∥ED.
18、已知:如图⊙O是Rt△CDE的外接圆,BC⊥CE,BD和CE的延长线交于点A,且OB∥ED. 26、已知:如图AD⊥BE,垂足C是BE的中点,AB=DE.AB与DE有何位置关系?请说明理由.
26、已知:如图AD⊥BE,垂足C是BE的中点,AB=DE.AB与DE有何位置关系?请说明理由. 已知:如图AB是半圆0的直径,点C在半圆上,CD⊥AB,垂足为D,切线PC交BA的延长线于点P,AD,DB的长是关于x的方程x2-(4m+2)+4m2=0(m>0)的两根,且AD:DB=1:4,求:PO、PC的长.
已知:如图AB是半圆0的直径,点C在半圆上,CD⊥AB,垂足为D,切线PC交BA的延长线于点P,AD,DB的长是关于x的方程x2-(4m+2)+4m2=0(m>0)的两根,且AD:DB=1:4,求:PO、PC的长.