题目内容
某公司有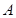 型产品40件,
型产品40件, 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
|
|
|
|
|
甲店 |
200 |
170 |
|
乙店 |
160 |
150 |
(1)设分配给甲店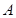 型产品
型产品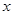 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为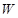 (元),求
(元),求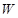 关于
关于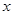 的函数关系式,并求出
的函数关系式,并求出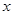 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店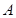 型产品让利销售,每件让利
型产品让利销售,每件让利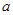 元,但让利后
元,但让利后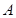 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店 型产品的每件利润.甲店的
型产品的每件利润.甲店的 型产品以及乙店的
型产品以及乙店的 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
依题意,甲店 型产品有
型产品有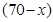 件,乙店
件,乙店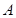 型有
型有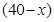 件,
件, 型有
型有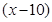 件,则
件,则
(1)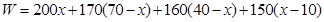
 .
.
由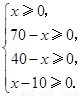 解得
解得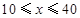 .
.
(2)由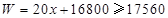 ,
,
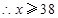 .
.
 ,
,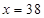 ,39,40.
,39,40.
 有三种不同的分配方案.
有三种不同的分配方案.
①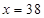 时,甲店
时,甲店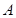 型38件,
型38件, 型32件,乙店
型32件,乙店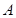 型2件,
型2件, 型28件.
型28件.
②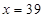 时,甲店
时,甲店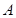 型39件,
型39件, 型31件,乙店
型31件,乙店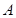 型1件,
型1件, 型29件.
型29件.
③ 时,甲店
时,甲店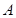 型40件,
型40件, 型30件,乙店
型30件,乙店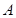 型0件,
型0件, 型30件.···· 3分
型30件.···· 3分
(3)依题意:
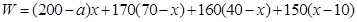
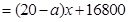 .
.
①当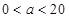 时,
时, ,即甲店
,即甲店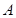 型40件,
型40件, 型30件,乙店
型30件,乙店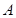 型0件,
型0件, 型30件,能使总利润达到最大.
型30件,能使总利润达到最大.
②当 时,
时,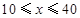 ,符合题意的各种方案,使总利润都一样.
,符合题意的各种方案,使总利润都一样.
③当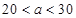 时,
时,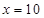 ,即甲店
,即甲店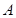 型10件,
型10件, 型60件,乙店
型60件,乙店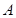 型30件,
型30件, 型0件,能使总利润达到最大.
4分
型0件,能使总利润达到最大.
4分
【解析】(1)根据所有产品数量及所给产品数量分别得到甲店B型商品,乙店A型商品,乙店B型商品的数量,那么总利润等于每件相应商品的利润×相应件数之和;根据各个店面的商品的数量为非负数可得自变量的取值;
(2)让(1)中的代数式≥17560,结合(1)中自变量的取值可得相应的分配方案;
(3)根据让利后A型产品的每件利润仍高于甲店B型产品的每件利润可得a的取值,结合(1)得到相应的总利润,根据a的不同取值得到利润的函数应得到的最大值的方案即可.

某公司有型产品40件,
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
|
|
|
|
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(1)设分配给甲店型产品
件,这家公司卖出这100件产品的总利润为
(元),求
关于
的函数关系式,并求出
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店型产品让利销售,每件让利
元,但让利后
型产品的每件利润仍高于甲店
型产品的每件利润.甲店的
型产品以及乙店的
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
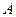 型产品40件,
型产品40件,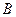 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:| | 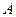 型利润 型利润 | 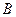 型利润 型利润 |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
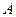 型产品
型产品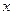 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为 (元),求
(元),求 关于
关于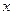 的函数关系式,并求出
的函数关系式,并求出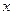 的取值范围;
的取值范围;(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店
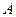 型产品让利销售,每件让利
型产品让利销售,每件让利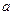 元,但让利后
元,但让利后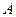 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店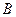 型产品的每件利润.甲店的
型产品的每件利润.甲店的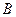 型产品以及乙店的
型产品以及乙店的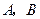 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大? 某公司有 型产品40件,
型产品40件, 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
| |  型利润 型利润 |  型利润 型利润 |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
 型产品
型产品 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为 (元),求
(元),求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 的取值范围;
的取值范围;(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店
 型产品让利销售,每件让利
型产品让利销售,每件让利 元,但让利后
元,但让利后 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店 型产品的每件利润.甲店的
型产品的每件利润.甲店的 型产品以及乙店的
型产品以及乙店的 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大? 某公司有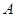 型产品40件,
型产品40件,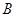 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
|
|
|
|
|
甲店 |
200 |
170 |
|
乙店 |
160 |
150 |
(1)设分配给甲店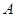 型产品
型产品 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为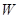 (元),求
(元),求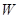 关于
关于 的函数关系式,并求出
的函数关系式,并求出 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店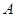 型产品让利销售,每件让利
型产品让利销售,每件让利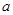 元,但让利后
元,但让利后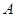 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店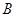 型产品的每件利润.甲店的
型产品的每件利润.甲店的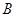 型产品以及乙店的
型产品以及乙店的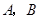 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?