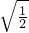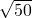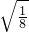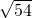题目内容
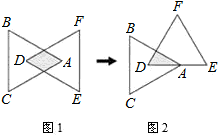 如图1,有两全等的正三角形ABC,DEF,且D,A分别为△ABC,△DEF的重心.固定D点,将△DEF逆时针旋转,使得A落在
如图1,有两全等的正三角形ABC,DEF,且D,A分别为△ABC,△DEF的重心.固定D点,将△DEF逆时针旋转,使得A落在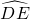 上,如图2所示.求图1与图2中,两个三角形重迭区域的面积比为何
上,如图2所示.求图1与图2中,两个三角形重迭区域的面积比为何
- A.2:1
- B.3:2
- C.4:3
- D.5:4
C
分析:设三角形的边长是x,则(1)中阴影部分是一个内角是60°的菱形,图(2)是个角是30°的直角三角形,分别求得两个图形的面积,即可求解.
解答: 解:设三角形的边长是x,则高长是
解:设三角形的边长是x,则高长是 x.
x.
图(1)中,阴影部分是一个内角是60°的菱形,AD= ×
× x=
x= x.
x.
另一条对角线长是:MN=2OM=2× OM•tan30°=2×
OM•tan30°=2× ×
× x•tan30°=
x•tan30°= x.
x.
则阴影部分的面积是: ×
× x•
x• x=
x= x2;
x2;
图(2)中,AD=AD= ×
× x=
x= x.
x.
是一个角是30°的直角三角形.
则阴影部分的面积= AD•sin30°•AD•cos30°=
AD•sin30°•AD•cos30°= ×
× x•×
x•× ×
× x•
x• =
=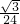 x2.
x2.
两个三角形重迭区域的面积比为: x2:
x2: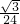 x2=4:3.
x2=4:3.
故选C.
点评:本题主要考查了三角形的重心的性质,解直角三角形,以及菱形、直角三角形面积的计算,正确计算两个图形的面积是解决本题的关键.
分析:设三角形的边长是x,则(1)中阴影部分是一个内角是60°的菱形,图(2)是个角是30°的直角三角形,分别求得两个图形的面积,即可求解.
解答:
 解:设三角形的边长是x,则高长是
解:设三角形的边长是x,则高长是 x.
x.图(1)中,阴影部分是一个内角是60°的菱形,AD=
 ×
× x=
x= x.
x.另一条对角线长是:MN=2OM=2×
 OM•tan30°=2×
OM•tan30°=2× ×
× x•tan30°=
x•tan30°= x.
x.则阴影部分的面积是:
 ×
× x•
x• x=
x= x2;
x2;图(2)中,AD=AD=
 ×
× x=
x= x.
x.是一个角是30°的直角三角形.
则阴影部分的面积=
 AD•sin30°•AD•cos30°=
AD•sin30°•AD•cos30°= ×
× x•×
x•× ×
× x•
x• =
=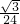 x2.
x2.两个三角形重迭区域的面积比为:
 x2:
x2: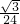 x2=4:3.
x2=4:3.故选C.
点评:本题主要考查了三角形的重心的性质,解直角三角形,以及菱形、直角三角形面积的计算,正确计算两个图形的面积是解决本题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
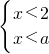 的解集是x<a,则a的取值范围是________.若不等式组
的解集是x<a,则a的取值范围是________.若不等式组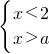 有4个整数解,则a的取值范围是________.
有4个整数解,则a的取值范围是________.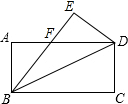 如图,在矩形ABCD中,AB=6,AD=8,将BC沿对角线BD对折,C点落在E点上,BE交AD于F,则AF的长为________.
如图,在矩形ABCD中,AB=6,AD=8,将BC沿对角线BD对折,C点落在E点上,BE交AD于F,则AF的长为________.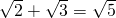
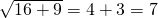
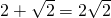
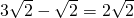
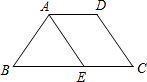 如图,等腰梯形ABCD中,AD∥BC,∠B=60°,E是BC上一点,AE∥DC,△ABE的周长为9,则等腰梯形的腰长是
如图,等腰梯形ABCD中,AD∥BC,∠B=60°,E是BC上一点,AE∥DC,△ABE的周长为9,则等腰梯形的腰长是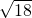 不是同类二次根式的是
不是同类二次根式的是