��Ŀ����
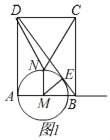
����Ŀ����ͼ1���ھ���ABCD�У�AB=9��BC=12����M�ӵ�A��������ÿ��2����λ���ȵ��ٶ���AB������AB���˶����Ե�MΪԲ�ģ�MA��Ϊ�뾶��Բ����ͼ2������M��NM��AB������M�ڵ�N�����˶�ʱ��Ϊt�룮
��1����գ�BD=�� ����BM=�� ����������ȷ��ֵ��t�Ĵ���ʽ��ʾ��
��2������M��BD����ʱ��
����t��ֵ��
������CDN�������
��3������CNDΪֱ��������ʱ�����t��ֵ��
���𰸡���1��15��9��t����2����t=2��36����3��t=4.5��
��������������(1)������Rt��ABD�Ĺ��ɶ������BD�ij��ȣ�����AM=t�ó�BM�ij��ȣ�(2)�١��жϳ���BME�͡�BDA���ƣ��ó�����ʽ�������̼��ɵó��𰸣��ڡ������MN��CD���ϵĸߣ����������ε������ʽ�ó��𰸣�(3)������N��ֱ��FG��MN���ֱ�AD��BC�ڵ�F��G���ֱ����![]() ��
��![]() ��t�Ĺ�ϵʽ��Ȼ�����DNC=90�����DCN=90������������t��ֵ��
��t�Ĺ�ϵʽ��Ȼ�����DNC=90�����DCN=90������������t��ֵ��
��⣺��1�����ı���ABCD�Ǿ��Σ� ��AD=BC=12����BAD=90�㣬
��Rt��ABD�У�AB=9��BC=12�����ݹ��ɶ����ã�BD=![]() =15��
=15��
���˶�֪��AM=t�� ��BM=AB��AM=9��t��
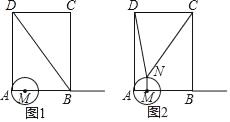
��2������ͼ1����M��BD��E�� ��ME��BD�� ���BEM=��BAD=90�㣬 �ߡ�EBM=��ABD��
���BME�ס�BDA�� ��![]() �� ��
�� ��![]() �� ��t=2��
�� ��t=2��
�ڡ�MN=AM=2t=4�� ��CD���ϵĸ�ΪAD��MN=12��4=8�� ��S��CDN=![]() ��9��8=36��
��9��8=36��
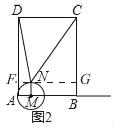
��3����ͼ2������N��ֱ��FG��MN���ֱ�AD��BC�ڵ�F��G��
��FN=2t��GN=9��2t��DF=CG=12��2t�� ��DN2=DF2+FN2=��12��2t��2+��2t��2��
��CN2=CG2+GN2=��12��2t��2+��9��2t��2��
������DNC=90��ʱ��DN2+CN2=CD2�� �ࣨ12��2t��2+��2t��2+��12��2t��2+��9��2t��2=81��
����4t2��33t+72=0�� �ߡ�=����33��2��4��4��72��0�� ���˷�����ʵ������
������DCN=90��ʱ����N��BC�ϣ�BN=BA=2t=9�� ��t=4.5��
����������t=4.5�룮