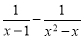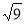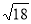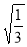Question

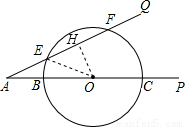
已知：如图，∠PAQ=30°，在边AP上顺次截取AB=3cm，BC=10cm，以BC为直径作⊙O交射线AQ于E、F两点，

求：（1）圆心O到AQ的距离；

（2）线段EF的长．

 

 

Answer 1

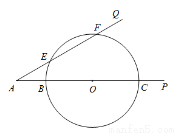
(1)即圆心O到AQ的距离为4cm；(2)EF=6cm.

【解析】

试题分析：

（1）过点O作OH⊥EF，垂足为点H，求出AO，根据含30度角的直角三角形性质求出即可；

（2）连接OE，根据勾股定理求出EH，根据垂径定理得出即可．

试题解析：

（1）过点O作OH⊥EF，垂足为点H，

∵OH⊥EF，

∴∠AHO=90°，

在Rt△AOH中，∵∠AHO=90°，∠PAQ=30°，

∴OH=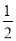AO，

∵BC=10cm，

∴BO=5cm．

∵AO=AB+BO，AB=3cm，

∴AO=3+5=8cm，

∴OH=4cm，即圆心O到AQ的距离为4cm．

（2）连接OE，

在Rt△EOH中，

∵∠EHO=90°，∴EH2+HO2=EO2，

∵EO=5cm，OH=4cm，

∴EH=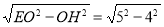=3cm，

∵OH过圆心O，OH⊥EF，

∴EF=2EH=6cm．

考点：垂径定理；含30度角的直角三角形；勾股定理．