题目内容
如图，在Rt△ABC中，∠BAC=90°，∠B=60°，△A
可以由△ABC绕点 A顺
时针旋转90°得到(点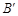
与点B是对应点，点
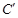与点C是对应点)，连接
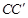，则∠
的度数是 .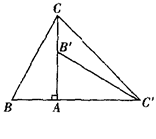
可以由△ABC绕点 A顺时针旋转90°得到(点
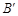与点B是对应点，点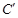与点C是对应点)，连接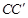，则∠的度数是 .
15°
由旋转的性质可知，AC=AC′，
又∠CAC′=90°，可知△CAC′为等腰直角三角形，
所以，∠CC′A=45°．∵∠CC′B′+∠ACC′=∠AB′C′=∠B=60°，∴∠CC′B′=15°．
又∠CAC′=90°，可知△CAC′为等腰直角三角形，
所以，∠CC′A=45°．∵∠CC′B′+∠ACC′=∠AB′C′=∠B=60°，∴∠CC′B′=15°．
练习册系列答案
相关题目
等于 度．
，5)关于y轴的对称点的坐标为（ ）
)
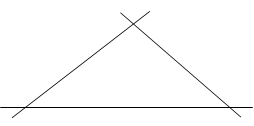
我们只要作点B关于l的对称点B′，（如图2所示）根据对称性可知，PB=PB＇．因此，求AP+BP最小就相当于求AP+PB′最小，显然当A、P、B′在一条直线上时AP+PB′最小，因此连接AB＇，与直线l的交点，就是要求的点P．
