题目内容
已知m是整数,且满足
,则关于x的方程m2x2-4x-2=(m+2)x2+3x+4的解为
|
x1=-
,x2=-2或x=-
| 3 |
| 2 |
| 6 |
| 7 |
x1=-
,x2=-2或x=-
.| 3 |
| 2 |
| 6 |
| 7 |
分析:先求出不等式组的解集,根据m是整数确定出m的值,然后代入关于x的方程,再利用因式分解法求解即可.
解答:解:
,
解不等式①得,m>
,
解不等式②得,m<3,
∴不等式组的解集是
<m<3,
∵m是整数,
∴m=1或2,
①当m=1时,方程可化为12x2-4x-2=(1+2)x2+3x+4,
即2x2+7x+6=0,
(2x+3)(x+2)=0,
∴2x+3=0,x+2=0,
解得x1=-
,x2=-2,
②当m=2时,方程可化为22x2-4x-2=(2+2)x2+3x+4,
即7x+6=0,
解得x=-
.
故答案为:x1=-
,x2=-2或x=-
.
|
解不等式①得,m>
| 1 |
| 2 |
解不等式②得,m<3,
∴不等式组的解集是
| 1 |
| 2 |
∵m是整数,
∴m=1或2,
①当m=1时,方程可化为12x2-4x-2=(1+2)x2+3x+4,
即2x2+7x+6=0,
(2x+3)(x+2)=0,
∴2x+3=0,x+2=0,
解得x1=-
| 3 |
| 2 |
②当m=2时,方程可化为22x2-4x-2=(2+2)x2+3x+4,
即7x+6=0,
解得x=-
| 6 |
| 7 |
故答案为:x1=-
| 3 |
| 2 |
| 6 |
| 7 |
点评:本题考查了一元一次不等式组的整数解,因式分解法解一元二次方程,确定出m的值是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知m是整数,且满足
,则关于x的方程m2x2-4x-2=(m+2)x2+3x+4的解为( )
|
A、x1=-2,x2=-
| ||||
B、x1=2,x2=
| ||||
C、x=-
| ||||
D、x1=-2,x2=-
|
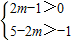 ,则关于x的方程m2x2-4x-2=(m+2)x2+3x+4的解为( )
,则关于x的方程m2x2-4x-2=(m+2)x2+3x+4的解为( )


 或x=-
或x=-