题目内容
已知△ABC中,AD是∠BAC的平分线,DE⊥AB,垂足是E,DF⊥AC,垂足是F,且△ABC的面积为28,AC=4,AB=10,则DE=分析:根据角平分线性质得出DE=DF,根据三角形的面积公式得出
AB×DE+
AC×DF=28,代入求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答: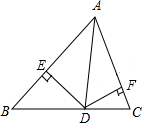 解:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
解:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵△ABC的面积为28,
∴S△ABD+S△ACD=28,
∴
AB×DE+
AC×DF=28,
即:10DE+4DE=56,
DE=4.
故答案为:4.
 解:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
解:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF,
∵△ABC的面积为28,
∴S△ABD+S△ACD=28,
∴
| 1 |
| 2 |
| 1 |
| 2 |
即:10DE+4DE=56,
DE=4.
故答案为:4.
点评:本题主要考查对三角形的面积,角平分线性质等知识点的理解和掌握,能求出DE=DF是解此题的关键.

练习册系列答案
相关题目
 如图,已知△ABC中,AD平分∠BAC交BC于D,AE⊥BC于E,若∠ADE=80°,∠EAC=20°,求∠B的度数.
如图,已知△ABC中,AD平分∠BAC交BC于D,AE⊥BC于E,若∠ADE=80°,∠EAC=20°,求∠B的度数. 已知△ABC中,AD⊥BC,E为BC上一点,EG∥AD,分别交AB和CA的延长线于F、G,∠AFG=∠G,
已知△ABC中,AD⊥BC,E为BC上一点,EG∥AD,分别交AB和CA的延长线于F、G,∠AFG=∠G, 如图,已知△ABC中,AD是BC边上的高,AE是∠BAC的角平分线,若∠C=40°,∠B=64°,求
如图,已知△ABC中,AD是BC边上的高,AE是∠BAC的角平分线,若∠C=40°,∠B=64°,求 已知△ABC中,AD平分∠BAC交BC于点D,E是线段AD上一点,EF⊥BC于点F,∠DEF=15°.
已知△ABC中,AD平分∠BAC交BC于点D,E是线段AD上一点,EF⊥BC于点F,∠DEF=15°.