题目内容
已知三角形两边长分别是1和2,第三边的长为2x2-5x+3=0的根,则这个三角形的周长是
- A.4
- B.
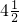
- C.4或
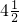
- D.不存在
B
分析:用十字相乘法因式分解,求出方程的两个根,分别是1和 ,再讨论三角形三边的关系,确定三角形第三边的长度,求出三角形的周长.
,再讨论三角形三边的关系,确定三角形第三边的长度,求出三角形的周长.
解答:2x2-5x+3=0,
(2x-3)(x-1)=0,
∴x1=1,x2= .
.
因为三角形两边长分别是1和2,则第三边长不能是1,只能是 ,
,
所以周长是4 .
.
故选B.
点评:本题考查的是用因式分解法解一元二次方程,求出方程的两个根,根据三角形三边的关系,确定方程的解中 是三角形的第三边,然后求出三角形的周长.
是三角形的第三边,然后求出三角形的周长.
分析:用十字相乘法因式分解,求出方程的两个根,分别是1和
 ,再讨论三角形三边的关系,确定三角形第三边的长度,求出三角形的周长.
,再讨论三角形三边的关系,确定三角形第三边的长度,求出三角形的周长.解答:2x2-5x+3=0,
(2x-3)(x-1)=0,
∴x1=1,x2=
 .
.因为三角形两边长分别是1和2,则第三边长不能是1,只能是
 ,
,所以周长是4
 .
.故选B.
点评:本题考查的是用因式分解法解一元二次方程,求出方程的两个根,根据三角形三边的关系,确定方程的解中
 是三角形的第三边,然后求出三角形的周长.
是三角形的第三边,然后求出三角形的周长. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目