Question

如图，有一圆弧形门拱的拱高AB为1m，跨度CD为4m，则这个门拱的半径为

 

m．

Answer 1

分析：连接OC，设这个门拱的半径为r，则OB=r-1，根据垂径定理得到BC=BD=

1

2

×CD，在Rt△OBC中，由勾股定理得OC²=BC²+OB²，然后即可得到关于r的方程，解方程即可求出r．

解答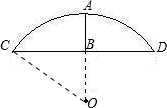：解：如图，连接OC，
设这个门拱的半径为r，则OB=r-1，
∴BC=BD=

1

2

×CD=

1

2

×4=2m
在Rt△OBC中，BC=2m，OB=r-1
由勾股定理得：OC²=BC²+OB²
即r²=4+（r-1）²
∴r=

5

2

m．
这个门拱的半径为

5

2

m．

点评：此题很简单，解答此题关键是连接OC，构造出直角三角形利用勾股定理解答．