Question

青岛国际帆船中心要修建一处公共服务设施，使它到三所运动员公寓A、B、C的距离相等．
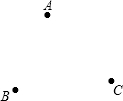
（1）若三所运动员公寓A、B、C的位置如图所示，请你在图中确定这处公共服务设施（用点P表示）的位置；
（2）若∠BAC=66°，则∠BPC=度．

Answer 1

解：（1）如图

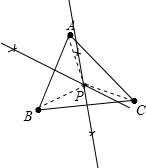
（2）连接点P和各顶点，以及AC．
∵PA=PB，
∴∠PAB=∠PBA，
同理∠PAC=∠PCA，
∵∠BAP+∠PAC=∠BAC=66°，
∴∠PAB+∠PBA+∠PAC+∠PCA=132°，
∵∠BPC+∠PBC+∠PCB=180°，
∴∠PAB+∠PBA+∠PAC+∠PCA+∠PBC+∠PCB=180°，
∴∠BPC=∠PAB+∠PBA+∠PAC+∠PCA=132°．
分析：（1）到线段两个端点距离相等的点应在线段的垂直平分线上，所以应作出任意两条线段的垂直平分线上；
（2）连接点P和各顶点，以及AC．根据线段的垂直平分线的性质和三角形的内角和定理求解．
点评：本题用到的知识点为：到线段两个端点距离相等的点应在线段的垂直平分线上；线段的垂直平分线上的点到线段的两个端点的距离相等．等边对等角．