题目内容
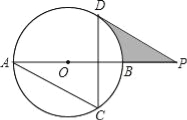
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]() cm2
cm2
【解析】
试题分析:(1)连接OD,求出∠AOD,求出∠DOB,求出∠ODP,根据切线判定推出即可;
(2)求出OP、DP长,分别求出扇形DOB和三角形ODP面积,即可求出答案.
试题解析:(1)连接OD,

∵∠ACD=60°,
∴由圆周角定理得:∠AOD=2∠ACD=120°,
∴∠DOP=180°﹣120°=60°,
∵∠APD=30°,
∴∠ODP=180°﹣30°﹣60°=90°,
∴OD⊥DP,
∵OD为半径,
∴DP是⊙O切线;
(2)∵∠P=30°,∠ODP=90°,OD=3cm,
∴OP=6cm,由勾股定理得:DP=3![]() cm,
cm,
∴图中阴影部分的面积S=S△ODP﹣S扇形DOB=![]() ×3×3
×3×3![]() ﹣
﹣![]() cm2
cm2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某中学研究性学习小组的同学们在社会实活动中调查了30户家庭某月的用水量,如表所示
用水量(吨) | 15 | 20 | 25 | 30 | 35 |
户数 | 3 | 6 | 7 | 9 | 5 |
这30户家该月用水量的众数和中位数分别是( )
A. 25,27.5B. 25,25C. 30,27.5D. 30,25