题目内容
【题目】填写下列空格,完成证明.
已知:如图,AD是△ABC的角平分线,点E在BC上,点F在CA的延长线上,EF∥AD,EF交AB于点G.
求证:∠3=∠F
证明:因为AD是△ABC的角平分线 ( 已知 )
所以∠1=∠2 ()
因为EF∥AD(已知)
所以∠3=∠()
∠F=∠()
所以∠3=∠F().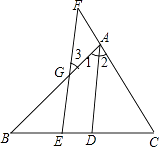
【答案】角平分线的定义;∠1;两直线平行,内错角相等;∠2;两直线平行,同位角相等;等量代换
【解析】证明:因为AD是△ABC的角平分线(已知 ),
所以∠1=∠2(角平分线的定义).
因为EF∥AD(已知),
所以∠3=∠1(两直线平行,内错角相等),∠F=∠2(两直线平行,同位角相等),
所以∠3=∠F(等量代换 ).
故答案为:角平分线的定义;∠1;两直线平行,内错角相等;∠2;两直线平行,同位角相等;等量代换.
根据角平分线的定义可得出∠1=∠2,再根据平行线的性质可得出∠3=∠1、∠F=∠2,进而即可得出∠3=∠F.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
【题目】下表是某种植物的种子在相同条件下发芽率试验的结果.
种子个数 | 100 | 400 | 900 | 1500 | 2500 | 4000 |
发芽种子个数 | 92 | 352 | 818 | 1336 | 2251 | 3601 |
发芽种子频率 | 0. 92 | 0. 88 | 0. 91 | 0. 89 | 0. 90 | 0. 90 |
根据上表中的数据,可估计该植物的种子发芽的概率为________.