题目内容
【题目】作图:

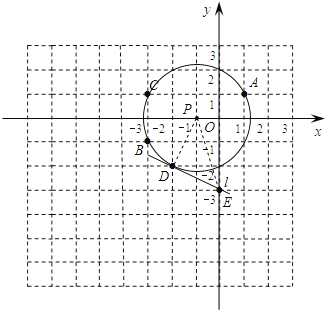
在同一平面直角坐标系中有5个点:A(1,1),B(﹣3,﹣1),C(﹣3,1),D(﹣2,﹣2),E(0,﹣3).
(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2)若直线l经过点D(﹣2,﹣2),E(0,﹣3),判断直线l与⊙P的位置关系.
【答案】(1)点D在⊙P上;(2)相切.
【解析】
试题分析:(1)在直角坐标系内描出各点,画出△ABC的外接圆,并指出点D与⊙P的位置关系即可;
(2)连接PE,用待定系数法求出直线PD与PE的位置关系即可.
试题解析:解:(1)如图所示:
△ABC外接圆的圆心为(﹣1,0),点D在⊙P上;
(2)连接PE,PD,∵直线 l过点 D(﹣2,﹣2 ),E (0,﹣3 ),∴![]() =10,
=10,![]() =5,
=5,![]() =5,,∴
=5,,∴![]() ,∴△PDE是直角三角形,且∠PDE=90°,∴PD⊥DE.∵点D在⊙P上,∴直线l与⊙P相切.
,∴△PDE是直角三角形,且∠PDE=90°,∴PD⊥DE.∵点D在⊙P上,∴直线l与⊙P相切.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目


