题目内容
【题目】材料阅读：
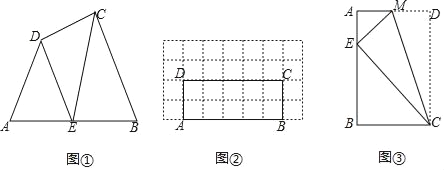
如图①，在四边形ABCD的边AB上任取一点E（点E不与点A、点B重合），分别连接ED，EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的强相似点．
解决问题：
（1）图①中，若∠A=∠B=∠DEC=40°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；
（2）如图②，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图②中画出矩形ABCD的边AB上的强相似点（无需写解答过程）；
（3）如图③所示的矩形ABCD，将矩形ABCD沿CM折叠后，点D落在AB边上的点E处，若点E恰好是四边形ABCM的边AB上的一个强相似点，试探究点E的位置．
【答案】（1）点E是四边形ABCD的边AB上的相似点；（2）详见解析；（3）E为AB的中点．
【解析】
（1）要证明点E是四边形ABCD的AB边上的相似点，只要证明有一组三角形相似就行，很容易证明△ADE∽△BEC，所以问题得解；
（2）以CD为直径画弧，取该弧与AB的一个交点即为所求；
（3）由点E是矩形ABCD的AB边上的一个强相似点，得△AEM∽△BCE∽△ECM，根据相似三角形的对应角相等，可求得∠BCE=
∠BCD=30°，利用含30°角的直角三角形性质可得BE与AB，边之间的数量关系，从而可求出E点的位置．
解：（1）点E是四边形ABCD的边AB上的相似点，理由是：
∵∠A=40°，
∴∠ADE+∠DEA=140°，
∵∠DEC=40°，
∴∠BEC+∠DEA=140°，
∴∠ADE=∠BEC，
∵∠A=∠B，
∴△ADE∽△BEC，
∴点E是四边形ABCD的边AB上的相似点；
（2）作图如下：
（3）若点E恰好是四边形ABCM的边AB上的一个强相似点，
则△AEM∽△BCE∽△ECM，
∴∠BCE=∠ECM=∠AEM，
由折叠得：∠ECM=∠DCM，CE=CD，
∴∠BCE=∠BCD=30°，
∴BE=
CE=AB，
即E为AB的中点．
