题目内容
【题目】如图,在△ABC中,AB=BC,∠ABC=100°,边BA绕点B顺时针旋转m°,(0<m<180)得到线段BD,连接AD、DC,若△ADC为等腰三角形,则m所有可能的取值是 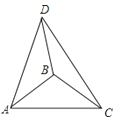
【答案】130或100或160
【解析】解:由旋转的性质得:BD=AB=BC,
∵△ADC为等腰三角形,
∴分三种情况:
①当DA=DC时,∠ABD=∠CBD=![]() (360°﹣∠ABC)=130°,
(360°﹣∠ABC)=130°,
∴m=130;
②当AD=AC时,∠ABD=∠ABC=100°,
∴m=100;
③当CA=CD时,∠CBD=∠ABC=100°,
∴∠ABD=360°﹣100°﹣100°=160°,
∴m=160;
综上所述:m所有可能的取值为130或100或160;
所以答案是:130或100或160.
【考点精析】本题主要考查了旋转的性质的相关知识点,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
