题目内容
P为边长为1的正方形ABCD的边CD的中点，点Q在BC上，当△ADP∽△QCP时，BQ=分析：根据题意画出图形，根据P是CD的中点求出DP及CP的长，再根据相似三角形的性质得出CQ的长，进而可求出BQ的长．
解答：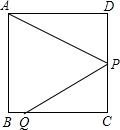
解：如图所示：
∵为边长为1的正方形ABCD的边CD的中点，
∴DP=CP=
，
∵△ADP∽△QCP，
∴
=
，
即
=
，
∴CQ=1，
∴Q与B点重合，
∴BQ=0．
故答案为：0．
解：如图所示：∵为边长为1的正方形ABCD的边CD的中点，
∴DP=CP=
| 1 |
| 2 |
∵△ADP∽△QCP，
∴
| AD |
| CQ |
| DP |
| CP |
即
| 1 |
| CQ |
| ||
|
∴CQ=1，
∴Q与B点重合，
∴BQ=0．
故答案为：0．
点评：本题考查的是正方形及相似三角形的性质，即相似三角形的对应边成比例．
练习册系列答案
相关题目
和
，顶点O所经过的路程是这两段圆弧的长度之和，并且这两段圆弧
?
和
，顶点O所经过的路程是这两段圆弧的长度之和，并且这两段圆弧
?
和
，顶点O所经过的路程是这两段圆弧的长度之和，并且这两段圆弧
?