题目内容
 如图,直线l过正方形ABCD的顶点A和BC边的中点E,点B到直线l的距离1,则D到l的距离是
如图,直线l过正方形ABCD的顶点A和BC边的中点E,点B到直线l的距离1,则D到l的距离是
- A.1.5
- B.2
- C.2.5
- D.3
B
分析:首先过点D,B,C作出垂直于l的线段DM,BN,CQ,利用全等三角形的判定与性质得出BN=CQ,再利用三角形相似判定方法得出△AMD∽△EQC,即可得出对应线段比例关系求出即可.
解答:过点D作DM⊥l于一点M,过点C作CQ⊥l于一点Q,过点B作BN⊥l于一点N,
∴∠AMD=∠BNE=∠CQE=90°,
∵E是BC的中点,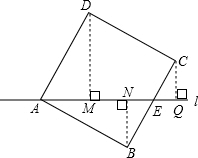
∴EC=BE,
∵∠BEN=∠CEQ,
∴△BNE≌△CQE,
∴BN=CQ=1,
∵四边形ABCD是正方形,
∴AD∥CE,
∴∠DAM=∠CEQ,
∵∠AND=∠EQC=90°,
∴△AMD∽△EQC,
∴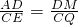 ,
,
∵CE=BE= BC,
BC,
∴CE= AD,
AD,
∴ ,
,
∴DM=2.
故选:B.
点评:此题主要考查了正方形的性质以及全等三角形的判定与性质和相似三角形的判定与性质等知识,正方形性质的考查经常与三角形的全等、以及三角形相似相结合综合考查,同学们分析问题时应多从这个角度思考.
分析:首先过点D,B,C作出垂直于l的线段DM,BN,CQ,利用全等三角形的判定与性质得出BN=CQ,再利用三角形相似判定方法得出△AMD∽△EQC,即可得出对应线段比例关系求出即可.
解答:过点D作DM⊥l于一点M,过点C作CQ⊥l于一点Q,过点B作BN⊥l于一点N,
∴∠AMD=∠BNE=∠CQE=90°,
∵E是BC的中点,

∴EC=BE,
∵∠BEN=∠CEQ,
∴△BNE≌△CQE,
∴BN=CQ=1,
∵四边形ABCD是正方形,
∴AD∥CE,
∴∠DAM=∠CEQ,
∵∠AND=∠EQC=90°,
∴△AMD∽△EQC,
∴
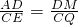 ,
,∵CE=BE=
 BC,
BC,∴CE=
 AD,
AD,∴
 ,
,∴DM=2.
故选:B.
点评:此题主要考查了正方形的性质以及全等三角形的判定与性质和相似三角形的判定与性质等知识,正方形性质的考查经常与三角形的全等、以及三角形相似相结合综合考查,同学们分析问题时应多从这个角度思考.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
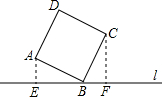 如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别为1和2,则正方形的边长是( )
如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别为1和2,则正方形的边长是( )| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
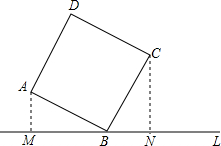 如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是
如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是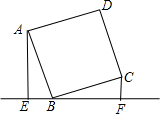 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是a和b,则正方形的边长是
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是a和b,则正方形的边长是 15、如图,直线l过正方形ABCD的顶点D,过A、C分别作直线l的垂线,垂足分别为E、F.若AE=4a,CF=a,则正方形ABCD的面积为
15、如图,直线l过正方形ABCD的顶点D,过A、C分别作直线l的垂线,垂足分别为E、F.若AE=4a,CF=a,则正方形ABCD的面积为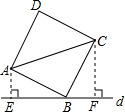 如图,直线d过正方形ABCD的顶点B,点A,C到直线d的距离分别是
如图,直线d过正方形ABCD的顶点B,点A,C到直线d的距离分别是